Bomber attack!

Classical Mechanics Level 2

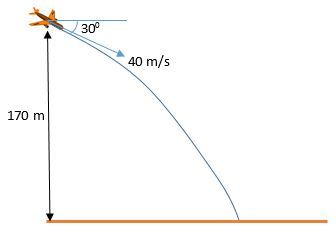
A bomber aircraft is flying at an altitude of 170 m \SI{170}{\meter} at an angle of 3 0 ∘ 30^\circ to the horizontal, as shown in the diagram. At time zero, it releases a bomb aimed at its target. After the release, how much time (in seconds) will the bomb take to hit the target? Give your answer to 2 decimal places.

Details and assumptions:

  • g = 10 m/s 2 g= 10 ~ \text{m/s}^2
  • v 0 = 40 m/s v_0 = 40 ~ \text{m/s}
  • Neglect air resistance.


The answer is 4.16.

Munem Shahriar by Munem Shahriar , 18, Bangladesh

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Arjen Vreugdenhil
Nov 29, 2017

In projectile motion we have y = y 0 + v y , 0 t + 1 2 g t 2 . y = y_0 + v_{y,0}t + \tfrac12gt^2. Substitute what we know: y 0 = 170 y_0 = 170 ; v y , 0 = − 40 sin ⁡ 3 0 ∘ = − 20 v_{y,0} = -40\sin 30^\circ = -20 ; g = − 10 g = -10 . Then y = 170 − 20 t − 5 t 2 . y = 170 - 20t - 5t^2. Impact happens when y = 0 y = 0 . We solve for t t . 170 − 20 t − 5 t 2 = 0 170 - 20t - 5t^2 = 0 t 2 + 4 t − 34 = 0 t^2 + 4t - 34 = 0 ( t + 2 ) 2 = 38 (t + 2)^2 = 38 t = − 2 ± 38 . t = -2\pm\sqrt{38}. We need the positive solution: t = − 2 + 38 ≈ 4.16. t = -2 + \sqrt{38} \approx 4.16.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...