Bored with congruent circles, yet?
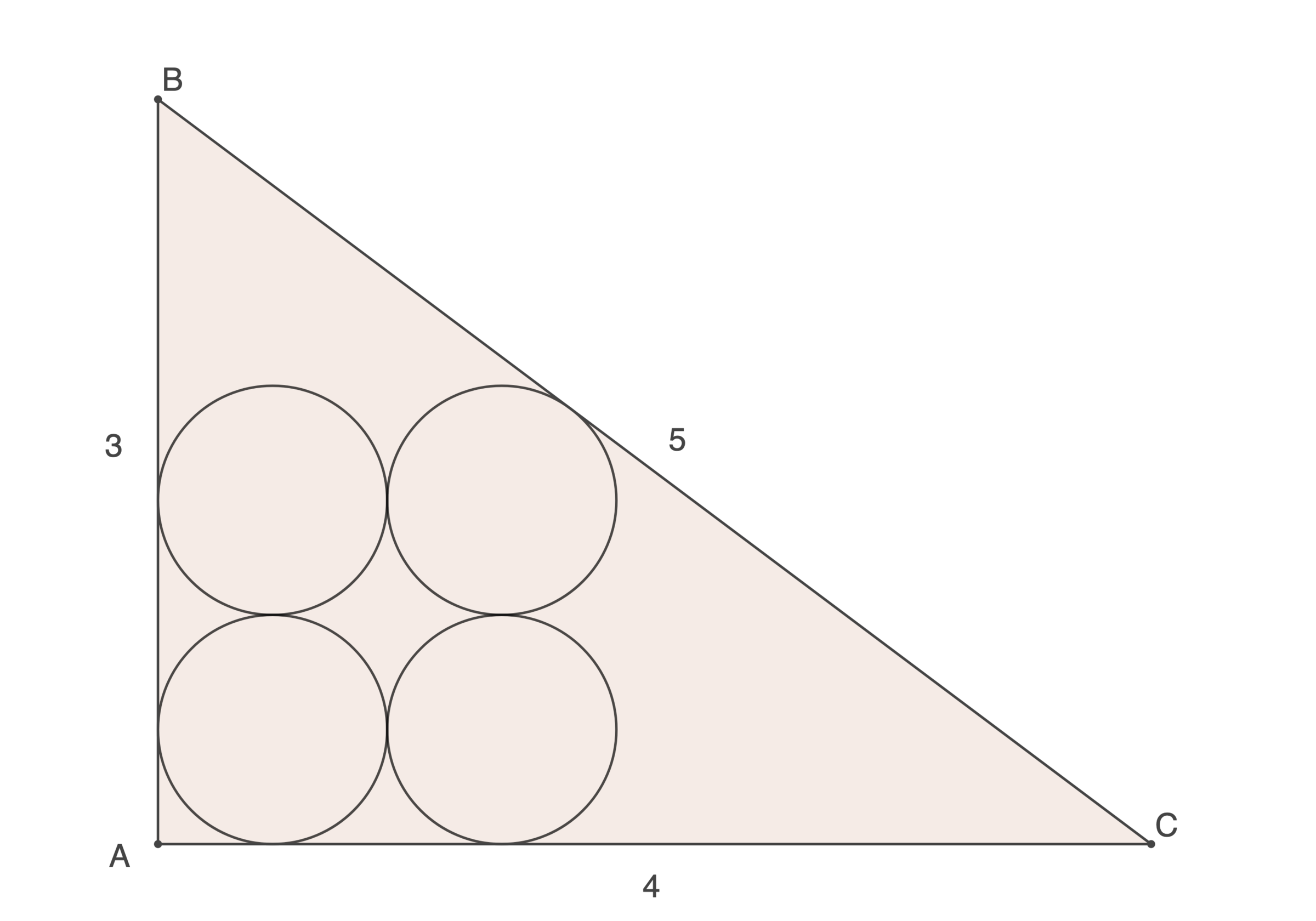
Given a 3-4-5 right triangle, find the radius of one of the four congruent circles as shown in the figure. If the radius is expressed as q p , where p and q are coprime positive integers, submit p + q .
Bonus: Generalise the solution for any right triangle in terms of the length of its legs.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice job, Chew-Seong. As always. Thank you.
Log in to reply
You are welcome. For this problem and others when the answer is b a , you have to mention positive coprime integers, because when both a and b are negative they are valid solution, so there will be two values for a + b .
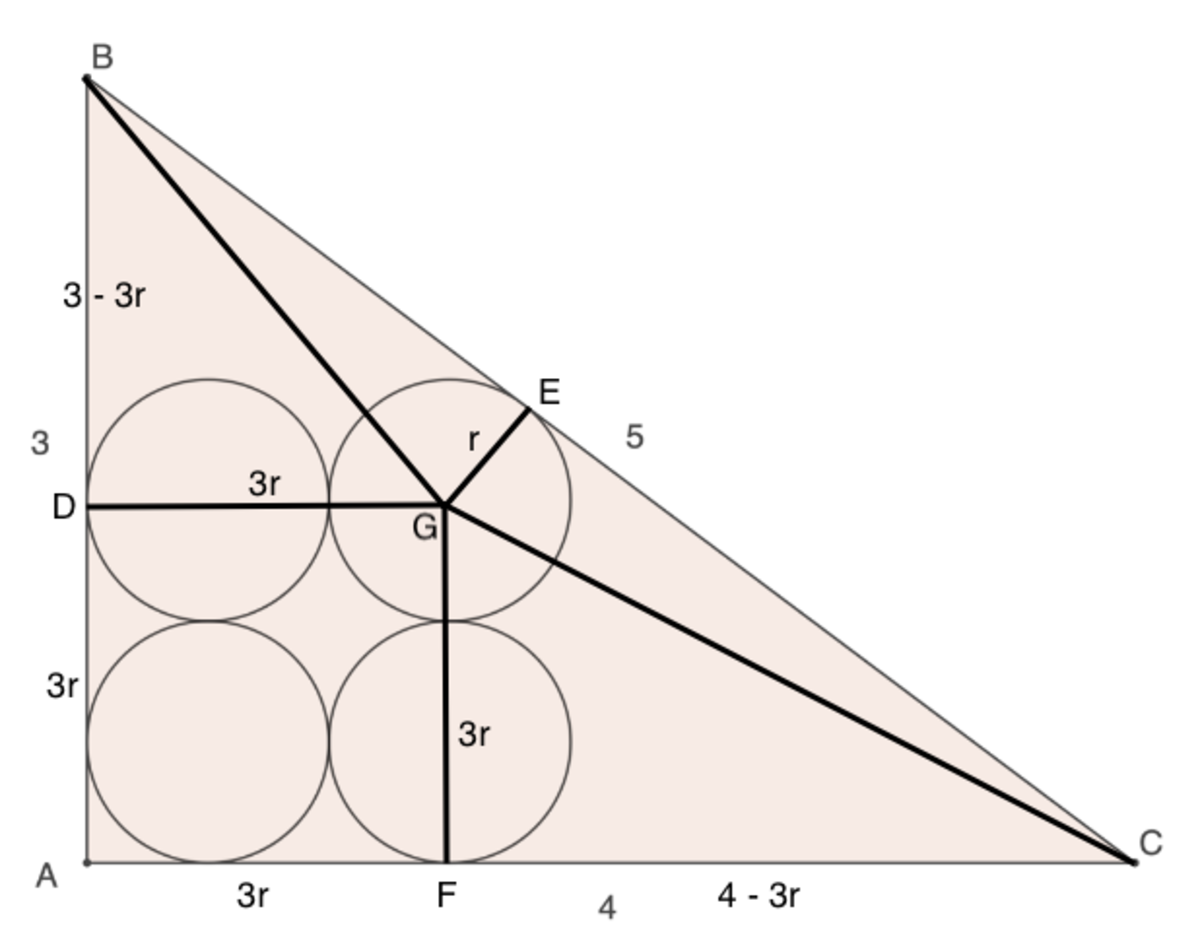
No trigonometry is needed. The area of Δ A B C can be written as Δ B G C + Δ B G D + Δ G F C + square A D G F , which can be expressed all in terms of r :
2 1 ( 5 r + ( 3 − 3 r ) ( 3 r ) + ( 4 − 3 r ) ( 3 r ) ) + ( 3 r ) 2 = 2 1 2 5 r + 2 1 r − 1 8 r 2 + 1 8 r 2 = 1 2 r = 5 + 2 1 1 2 = 1 3 6
Hence p + q = 6 + 1 3 = 1 9 .
Labelling the triangle's sides the same as Chew-Seong does, we get that a r + 3 c r + 3 b r = a b ⇒ r = a + 3 ( b + c ) b c in general.
Actually if you connect A and G, then the equation becomes: 2 1 × ( 3 r × 4 + 3 r × 3 + r × 5 ) = 6
Log in to reply
That's even better! From here, we get r = 2 6 1 2 = 1 3 6 more directly.
Exactly my first thought: why not divide that's square? But anyhow it's still a very nice solution!
I think this is an ingeneous and creative solution @Toby M . Good work. I think you meant to say △ A B C not △ A B C D .
There are two solutions r= 6/13 and r=3/4 to the equation ✓[(3-3r)^2+(3r)^2-r^2]+ ✓[(4-3r)^2+(3r)^2-r^2]=5.
Answer = 19
Consider a general right triangle with side lengths a , b , and c . Let the radius of the four congruent circles be r and ∠ C = θ . Also D E be the line passing through the centers right two circles, which is perpendicular to A C . Then D E = r sec θ + 3 r and E C = b − 3 r . Now we have:
E C D E b − 3 r r sec θ + 3 r b − 3 r b a r + 3 r a r + 3 b r ⟹ r = tan θ = tan θ = b c = b c − 3 c r = a + 3 ( b + c ) b c Note that sec θ = b a and tan θ = b c
For a = 5 , b = 4 , and c = 3 , r = 5 + 3 ( 4 + 3 ) 4 × 3 = 2 6 1 2 = 1 3 6 . Then a + b = 6 + 1 3 = 1 9 .