Bounce one more time!
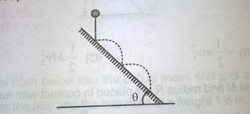A ball is released from a height H above an inclined plane and makes several bounces . The angle of inclination of plane is
. Assume that the ball bounces elastically in each hit . Find the distance from the first hit to fourth hit on the inclined plane.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
let the velocity of the ball just before the collision be v1 along the incline and v2 perpendicular to the incline...(where ((v1^2)+(v2^2))=2gH) and g1 be the component of g along the incline and g2 be the component of g perpendicular to the incline.
total no. of bounces =3 calculation of time taken for half bounce : using equation of motion v=u+at here 0=v2-(g2)t t=v2/g2 time taken for 3 bounces= 6*(v2/g2)=T
distance travelled along the incline .by the equation s=ut+1/2at^2 here
u=v1 t=T a=g1
PUTTING THE VALUES WE GET s= 48Hsin(theta)