Bouncing around
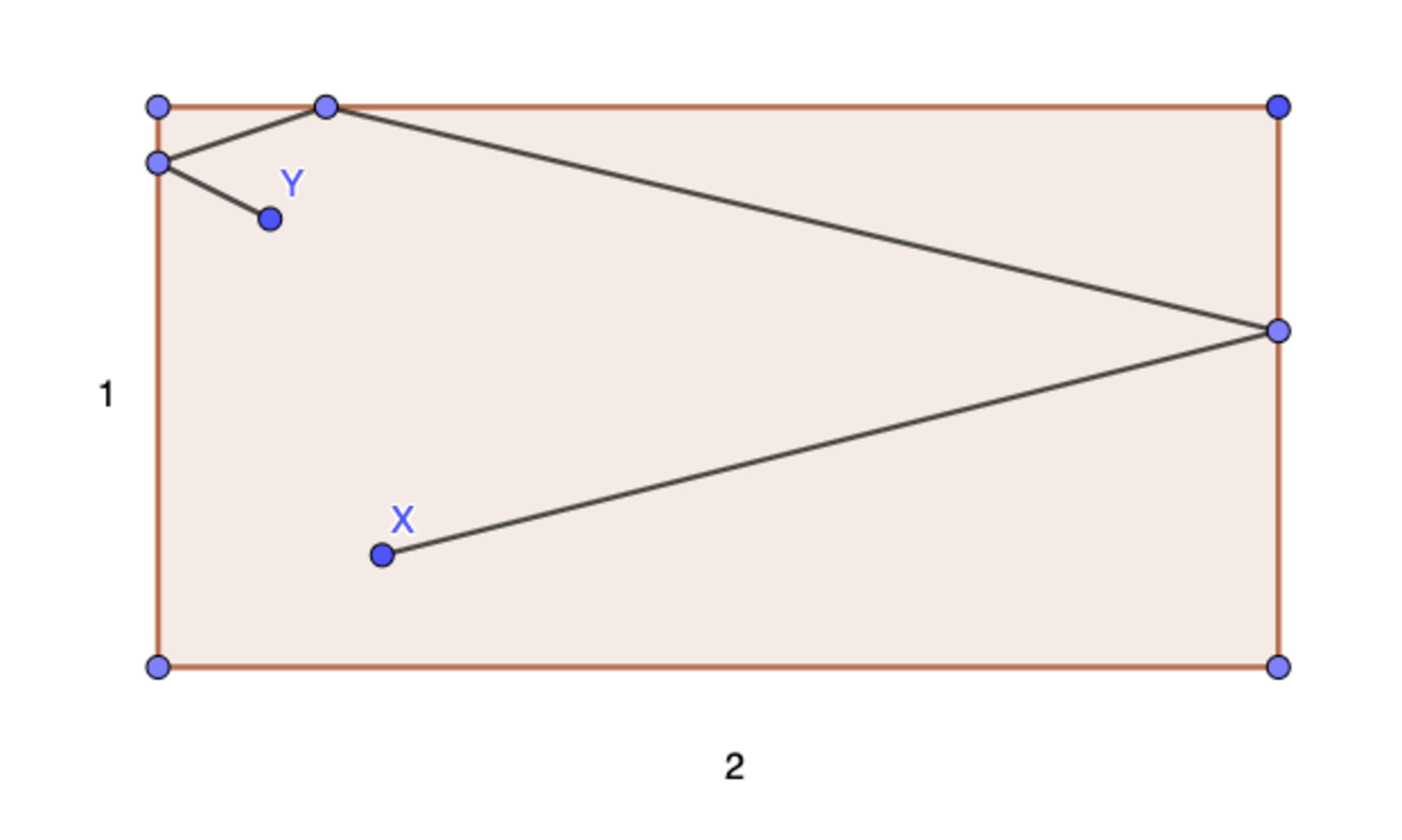 A ball start at a pool table at the point
X
(the table 1" wide , 2" long) , then a man shoot it to the right and then it bounce to the top and then left , finally , it stoped at the point
Y
. And we know that
X
is 0.6" to the left and 0.2" to the bottom .
Y
is 0.2" from the left and 0.25" from the top . If the ball always rebounds at the same angle as it hits the side , then what is the distance the ball moves?
A ball start at a pool table at the point
X
(the table 1" wide , 2" long) , then a man shoot it to the right and then it bounce to the top and then left , finally , it stoped at the point
Y
. And we know that
X
is 0.6" to the left and 0.2" to the bottom .
Y
is 0.2" from the left and 0.25" from the top . If the ball always rebounds at the same angle as it hits the side , then what is the distance the ball moves?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
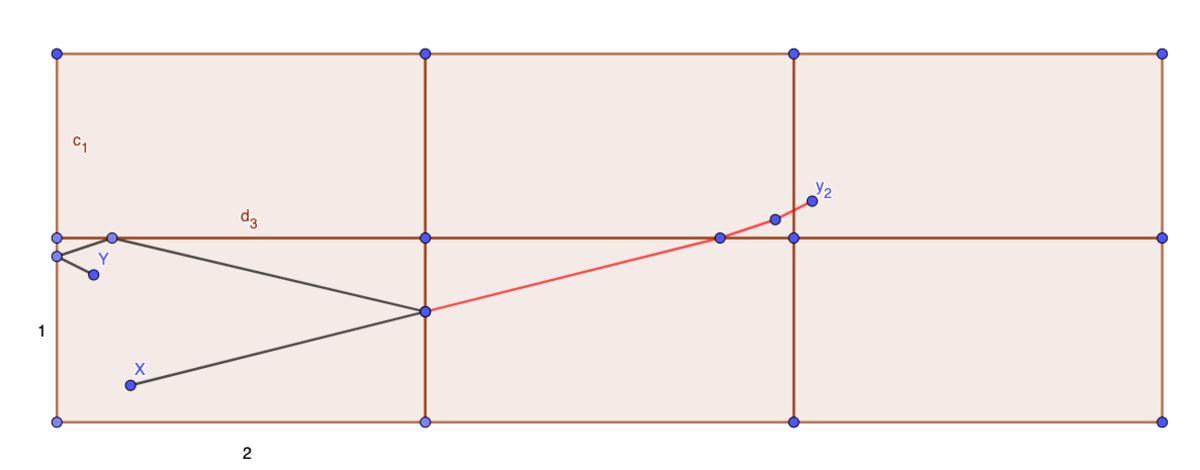 Just unfold it!
Using the Pythagorean theorem you can figure out the distance is √[(2 + 2 - 0.6 + 0.2)
2
+ (1 - 0.2 + 0.25)] = 3.75".
Just unfold it!
Using the Pythagorean theorem you can figure out the distance is √[(2 + 2 - 0.6 + 0.2)
2
+ (1 - 0.2 + 0.25)] = 3.75".
Let the angle of incidence in the case of first reflection be α . Then, after some calculation work we get the equation :
3 . 6 tan α = 1 . 0 5 ⟹ tan α = 3 . 6 1 . 0 5 ⟹ sec α = 1 + tan 2 α = 3 . 6 3 . 7 5 .
Hence the length of total path covered is
1 . 4 sec α + ( 0 . 8 − 1 . 4 tan α ) cosec α + ( 3 . 4 tan α − 0 . 8 ) cosec α + 0 . 2 sec α = 3 . 6 sec α = 3 . 7 5 ′ ′ .