Bouncing back

Relevant wiki: Mirrors

One can "unfold" each reflection, so that the path of the light is straight, but it intersects with the mirror images of the mirrors. This is illustrated in the Figure below (we used an angle that is larger than $17^{\circ}$ ). Here the light makes 3 bounces, because the 4th one would be on the red mirror that makes more than $180^{\circ}$ with the original light path. For our numbers 10 bounces leads to $170^{\circ}$ and the next one is impossible, $187^{\circ}$ .

Relevant wiki: Mirrors

Two plane mirrors (shown to the right) both stand perpendicular to the floor and meet at the angle $\theta = 17 ^ \circ$

How can the mirrors both

• stand perpendicular to the floor

  and

• meet

Edit: To address the "top view" arguments in the comments - Perpendicular means:

When the two planes $\alpha$ and $\beta$ are perpendicular, their normal vectors are also perpendicular and their dot product is 0.

So if both mirrors are standing with their normal's perpendicular with that of the floor, then the mirrors can never meet. Their normal's would also be parallel.

In the question, as implied, the normal's of the mirrors are not both perpendicular with the floor, nor are the normal's parallel with each other.

The question needs rewording. For example:

Two plane mirrors rest on a flat surface, meeting each other along one edge at an angle of $\theta = 17 ^ \circ$

Relevant wiki: Reflection

Let $\theta$ be the angle between the direction of the light and the vertical (counterclockwise = positive). Initially, $\theta = 0$ .

Reflection in the first mirror results in $R_1:\ \theta \mapsto -\theta$ ; reflection in the second, $R_2:\ \theta \mapsto 34-\theta$ . (This is the only way in which $17^\circ$ is mapped to itself.)

After a reflection, the beam will not bounce off the same mirror again. Thus we get alternating applications of $R_1$ and $R_2$ , starting with $R_2$ .

We find that

• after $2n-1$ reflections, the beam has direction $34n$ ;

• after $2n$ reflections, the beam has direction $-34n$ .

The beam will stop bouncing when it is directed away from both mirrors, i.e. $-180^\circ < \theta < -163^\circ$ . This happens when $n = 5$ :

• after $2\cdot 5 = \boxed{10}$ reflections, the beam has direction $-34\cdot 5 = -170^\circ$ .

Let x = 17°. Laser is falling on 1st mirror at an angle x, after reflection, it would fall on 2nd at an angle 2x, then on 1st at 3x and so on till it reaches 5x = 85.
Thereafter 6x = 102 > 90°, at this point, the laser rays reverse direction and return journey begins, rays would fall on 2nd mirror at (180 - 6x)°. Then on 1st at (180 - 7x), then (180 - 8x) and so on till it falls at (180 - 10x) = 10° on 2nd. Thereafter since the angle is less than 17°, Laser can not fall on 1st mirror and escapes.
So, light is reflected 5 times from x to 5x, and 5 times from (180 - 6x) to (180 - 10x),
total 10 times.

• Fact 1: The mirror on the left is "straight", and intersects the mirror on the right, which is "diagonal."
• Fact 2: Mirrors reflect. When light hits a mirror, it inverts the light. So if a laser hits a mirror at 10 $^\circ$ from the left, it will reflect 10 $^\circ$ to the right.
• Fact 3: The left mirror intersects the diagonal mirror at 17 $^\circ$ .
• Fact 4: The laser emits a "straight" beam of light, parallel to the left mirror.
• Fact 5: The internal angle of all Triangles is 180 $^\circ$ .
• Fact 6: A right angle has one 90 degree angle. Squares have 4 right angles, Triangles have 1.
• Fact 7: If a light hits a mirror at 90 $^\circ$ (Perpendicular), it will reflect directly back at itself.

Figure 1. Because of facts 3 and 4, we can assume the angle of the laser's intersection with the diagonal mirror is 17 $^\circ$ .

Figure 2: Following the laser THROUGH the mirror, and reviewing the Reflection, in accordance with Fact 2, Figure 2 shows that five angles are created. The important three are the three 17 degree angles.

Figure 3: The first step to discovery is important, and different than the rest of the steps. Fact 5 says the internal angles of all Triangles always equals 180 $^\circ$ .. Using Fact 6, we can create a Right-Triangle, determine two of the angles, and calculate the third. You can easily create a Right-Triangle, and Square, using the left mirror and drawing a line to the point of intersection. Given that the bottom-left angle is 90, and the bottom-right angle is 90 - 17 - 17 = 56. Knowing the two angles, we know the third angle is 34 because 180 - (90 + 56).

Figure 4: Back to using Fact 2, because the laser's second point of impact is against the left mirror at 34 $^\circ$ . from the bottom, we can assert that it will reflect with an angle of 34 $^\circ$ . at the top.

Figure 5: Given facts 5 and 6, we can determine the angle of reflection on point of impact 3 against the right mirror. Since we know the first angle is 17, and the INSIDE of the second angle is 112 (180 - (34 + 34)), we know the angle of the third point of impact is 51.

If we repeat Figure 5 a few times, we get the following angles:

• Point 1: 17 $^\circ$ .
• Point 2: 34 $^\circ$ .
• Point 3: 51 $^\circ$ .
• Point 4: 68 $^\circ$ .
• Point 5: 85 $^\circ$ . (Uh oh . . . almost past 90 $^\circ$ .)
• Point 6: 102 $^\circ$ . (BAM)

Given Fact 7, and the fact that we have SURPASSED the 90 degree rule, we have now flipped the direction and begun backing out of our crevasse.

Figure 6: At some point in the process you might pick up on the pattern that each angle increases by the angle we started with. So if our first angle of x is 17, then our second angle of x is 2x, or 2 17, and our third angle is 3x (3 17=51), and so forth. But we have a problem when we surpass 90 $^\circ$ ., that we need to reverse our angles so we can continue our math. The result is negative (180 - (102 + 102)) = -24.

But knowing the inside angle as -24 (or 24 as the absolute value), we know that the top and bottom angles are 78 and 78 (78 + 78 + 24 = 180). So we now know our approach back down our crevasse.

Figure 7: If we reverse our discovery of adding 17 to the prior lesson, we find these angles:

• Point 6: 78 $^\circ$ . (Revised to be the inverse, less than 90)
• Point 7: 61 $^\circ$ . - point of impact is on the right (diagonal) mirror
• Point 8: 44 $^\circ$ . - point of impact is on the left mirror
• Point 9: 27 $^\circ$ . - point of impact is on the right (diagonal) mirror
• Point 10: 10 $^\circ$ . - point of impact is on the left mirror

Because the 10th point leaves the left mirror at 10 $^\circ$ ., and the right (diagonal) mirror is angled away at 17 $^\circ$ ., the new vector of the laser will never again hit the right or left mirrors.

Given what we know, we can say that the initial angle of 17, multiplied by 10 points of intersection, is 170 (Less than 180). If it were to go any more, the angle would exceed 180, so it fails. Therefore, if the angle were 19 $^\circ$ ., it would only intersect 9 times, because the tenth time would be more than 180 $^\circ$ ..

This allows us to determine, for the future, that if the angle of approach of the first laser is parallel to one of the sides, then the degree of interception can be divided into 180 degrees, and the floor is the number of points of intersection.

Figures: 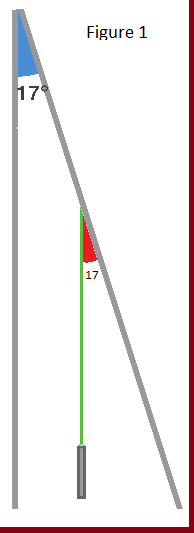Figure 1 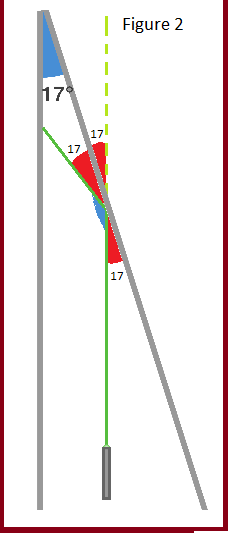Figure 2 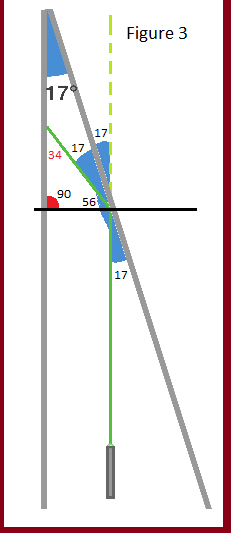Figure 3 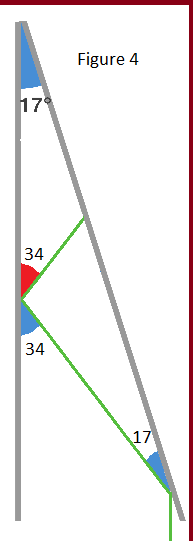Figure 4 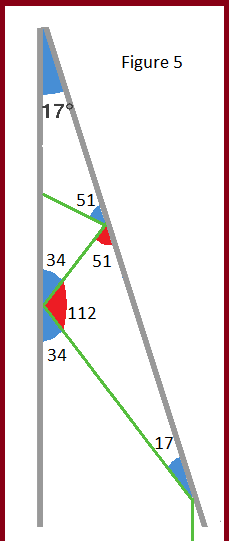Figure 5 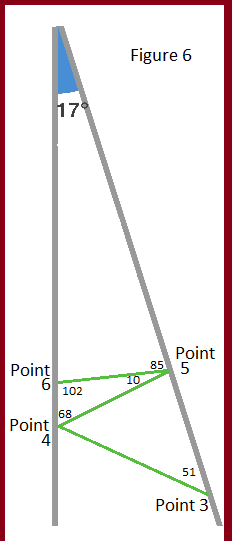Figure 6 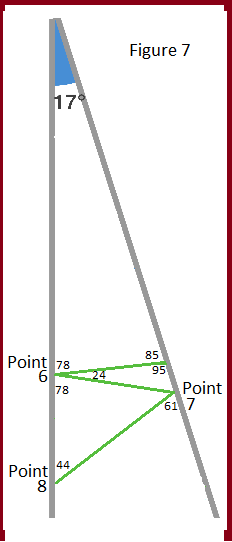Figure 7

Just divide 17 into 180 - get 10 plus a fraction - eliminate the fraction.

Just use the formula 180/angle For this case 180/17 =10. This formula is easily derived.