Bouncing Ball

Algebra Level 3

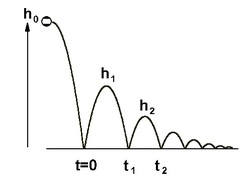A ball is dropped from the height of 10 m on a horizontal floor and bounces back half the distance from the previous bounce and keeps on bouncing for ever.
Find the total vertical distance (in m) covered by the ball.

Details:

Neglect the air resistance and any other dissipating force.

The answer is 30.

3 solutions

Chew-Seong Cheong
Sep 20, 2015

The vertical distance covered by the ball was:

$\begin{aligned} D & = 10 + (5 \times 2) + \left( \frac{5}{2} \times 2 \right) + \left( \frac{5}{4} \times 2 \right) + \left( \frac{5}{8} \times 2 \right) + ... \\ & = 10 + 10 + 5 + \frac{5}{2} + \frac{5}{4} + ... \\ & = 10 + 10 \sum_{n=0}^\infty \left(\frac{1}{2}\right)^n \\ & = 10 + 10 \left(\frac{1}{1-\frac{1}{2}} \right) \\ & = 10 + 10(2) \\ & = \boxed{30} \end{aligned}$

Sorry, I don't understand. Shouldn't it just be 10+5+2.5+...... which is equal to 20?

Raghav Arora - 5 years, 8 months ago

Step 1 : 10 m downward.
Step 2 : 5 m upwards.
Step 3 : 5 m downward.
Step 4 : 2.5 m upward.
Step 5 : 2.5 m downward.
$\quad\quad$ $\vdots$
$\quad \quad$ $\vdots$
$\quad\quad$ $\infty$
$\text{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}$
$\quad$ Total : 30 m

Akhil Bansal - 5 years, 8 months ago

Aakash Khandelwal
Sep 20, 2015

Total height is he^2 + h/ 1-e^2 Where h is height from where it is dropped and e is coefficient of restitution. e^2 = a/h where 'a'is the height two which ball rises after furst collision with ground. Hence e^2 is 0.5 . And total height is 3h = 30m

Kshitij Goel
Sep 19, 2015

If we will notice the pattern then we will find that total height is

10+2(5)+2(2.5)+2(1.25).......

10+2{5+2.5+1.25.........} 10+2{5(1)+5(1÷2)+5(1÷4)+.......+..} 10+10{1+(1÷2)+(1÷4).....} On applying the formula of geometric progression 1+(1÷2)+(1÷4)....=2 So answer is 10+10(2) 10+20 30

Bouncing Ball

The answer is 30.

3 solutions

0 pending reports