Bouncing Between Rings
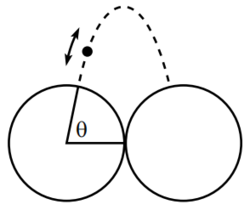
Two fixed circular rings, in contact with each other, stand in a vertical plane. A ball bounces elastically back and forth between the rings. Assume that air resistance is negligible and initial conditions have been set up so that the ball’s motion forever lies in one parabola. Let this parabola hit the rings at an angle from the horizontal.
What should be, so that the magnitude of the change in the horizontal component of the ball’s momentum at each bounce is maximum?
If the answer can be written as find the value of
The answer is 0.618034.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The collision is elastic with no other forms of resistance , so the ball will bounce with the same magnitude of horizontal velocity v x
the magnitude of the change in the horizontal component of the ball’s momentum , Δ p = 2 m v x
d = 2 r ( 1 − c o s θ )
t = v x x ( t ) ........................(1)
y ( t ) = v y t − 2 1 g t 2 ..........(2)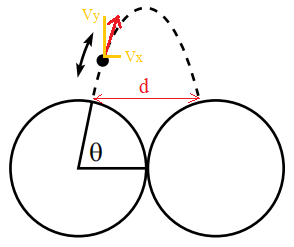
at t = v x d , y ( t ) = 0 , ... sub. into eq.(2) ,
0 = v y v x d − 2 g ( v x d ) 2
v x = v y g d = 2 v s i n θ 2 g r ( 1 − c o s θ ) = v s i n θ g r ( 1 − c o s θ )
but v = c o s θ v x
( v x c o s θ ) 2 = t a n θ g r ( 1 − c o s θ )
Now, to find the magnitude of angle θ at which v x is maximum we differentiate the above equation W.R.T θ and equate the result to zero ,
d θ d ( v x c o s θ ) 2 = g r t a n 2 θ s i n θ t a n θ − ( 1 − c o s θ ) s e c 2 θ = 0
s i n θ t a n θ − ( 1 − c o s θ ) s e c 2 θ = 0
( 1 − c o s θ ) ( c o s θ ( 1 + c o s θ ) − 1 ) = 0
Either ( 1 − c o s θ ) = 0 , θ = 0 , π , 2 π , . . . Neglected
Or c o s θ ( 1 + c o s θ ) − 1 = 0 ==> θ = 2 5 − 1 ≈ 0 . 6 1 8 YES , we can see the finger print of Golden ratio