Bouncing Between Surfaces

Classical Mechanics Level 3

Consider the following generalization of the previous problem .

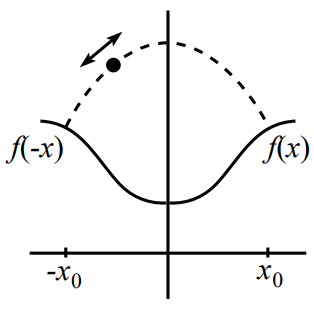
Now let a ball bounce back and forth between a surface defined by $f(x)$ (for $x>0$ ) and its reflection across the $y$ -axis $f(-x)$ (for $x<0).$ Assume that initial conditions have been set up so that the ball’s motion forever lies in one parabola, with the contact points $(x_0,f(x_0))$ and $(-x_0,f(x_0)).$

For what function $f(x)$ is the magnitude of the change in the horizontal component of the ball’s momentum at each bounce independent of $x_0?$

f(x)=a\ln x+b,a>0

f(x)=ax^2+b,a>0

f(x)=-\frac ax+b,a>0

f(x)=ae^x+b,a>0

1 solution

K T
Feb 25, 2019

Assume that we can neglect the ball's size.

Let the coordinates be such that the highest point is reached at $x=0, y=y_0, t=0$ .

The motion of the ball then is described by the parametrization

$y(t)=y_0-\frac{1}{2}gt^2$

$x(t)=v_x t$ .

Substituting $t=\frac{x}{v_x}$ into the expression for y, reveals that the shape of the parabola is defined by

$y(x)=y_0-\frac{1}{2}g\frac{x^2}{v_x^2}$ .

Hence we have $\frac{dy}{dx}= \frac{-gx}{v_x^2}$ .

f(x) must be perpendicular to this, so that $f'(x)= \frac{v_x^2}{gx}$ .

If the horizontal momentum $mv_x$ is independent of x, $v_x$ can be considered a constant.

Suppose $f(x)=a \ln|x|+b$ , then $f'(x)=\frac{a}{x}$ so that our function is given by

$f(x)= \frac{v_x^2}{g} \ln|x|+b$ where b is an arbitrary constant.

Bouncing Between Surfaces

1 solution

0 pending reports