Bouncing DVD Logo
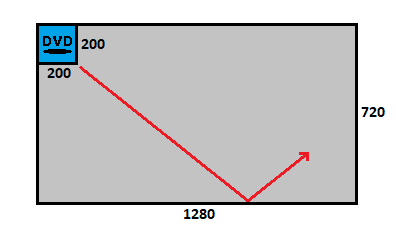
A 200 x 200 pixel DVD logo starts in the top left corner of a 1280 x 720 pixel screen and travels down and to the right at a slope of
, obeying the laws of reflection whenever it reaches any edge of the screen and so that the entirety of the DVD logo can be seen on the screen at all times. If it takes the DVD logo 10 seconds to travel from its furthest rightmost position to its furthest leftmost position, and the DVD logo travels at a constant speed, how many seconds will it take the DVD logo to reach the next of any one of the screen’s exact corners?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since the entirety of the DVD logo can be seen at all times, any point on the 200 x 200 pixel DVD logo is really just bouncing inside of a (1280 – 200) x (720 – 200) = 1080 x 520 boundary rectangle.
As given in the problem, the DVD logo reflects off either a right or left wall every t = 1 0 seconds. Visualizing the path of the DVD logo as a straight line through a series of reflections of the boundary rectangle, as shown below, the DVD logo reflects off either a bottom or top wall every t = distance / speed = 4 5 ( 5 2 0 ) / ( 1 0 1 0 8 0 ) = 5 4 3 2 5 seconds (or t ≈ 6 . 0 2 seconds).
The DVD logo will therefore reach the next corner (an intersection of a top or bottom wall with a left or right wall) at the least common multiple of 10 and 5 4 3 2 5 , which is t = 6 5 0 seconds.