Bouncing Inside a Box
A square box is fixed in place in the plane, with its corners at values of , , , and . A ball is initially at , with a velocity vector of . The ball bounces off of the sides of the box.
What is the sum of the and coordinates of the ball on its 1000th bounce?
Details and Assumptions:
- When the ball bounces off of a horizontal surface, its
velocity is negated and its
velocity is preserved.
- When the ball bounces off of a vertical surface, its
velocity is negated and its
velocity is preserved.
- There are no forces at play when the ball is traversing the interior of the box
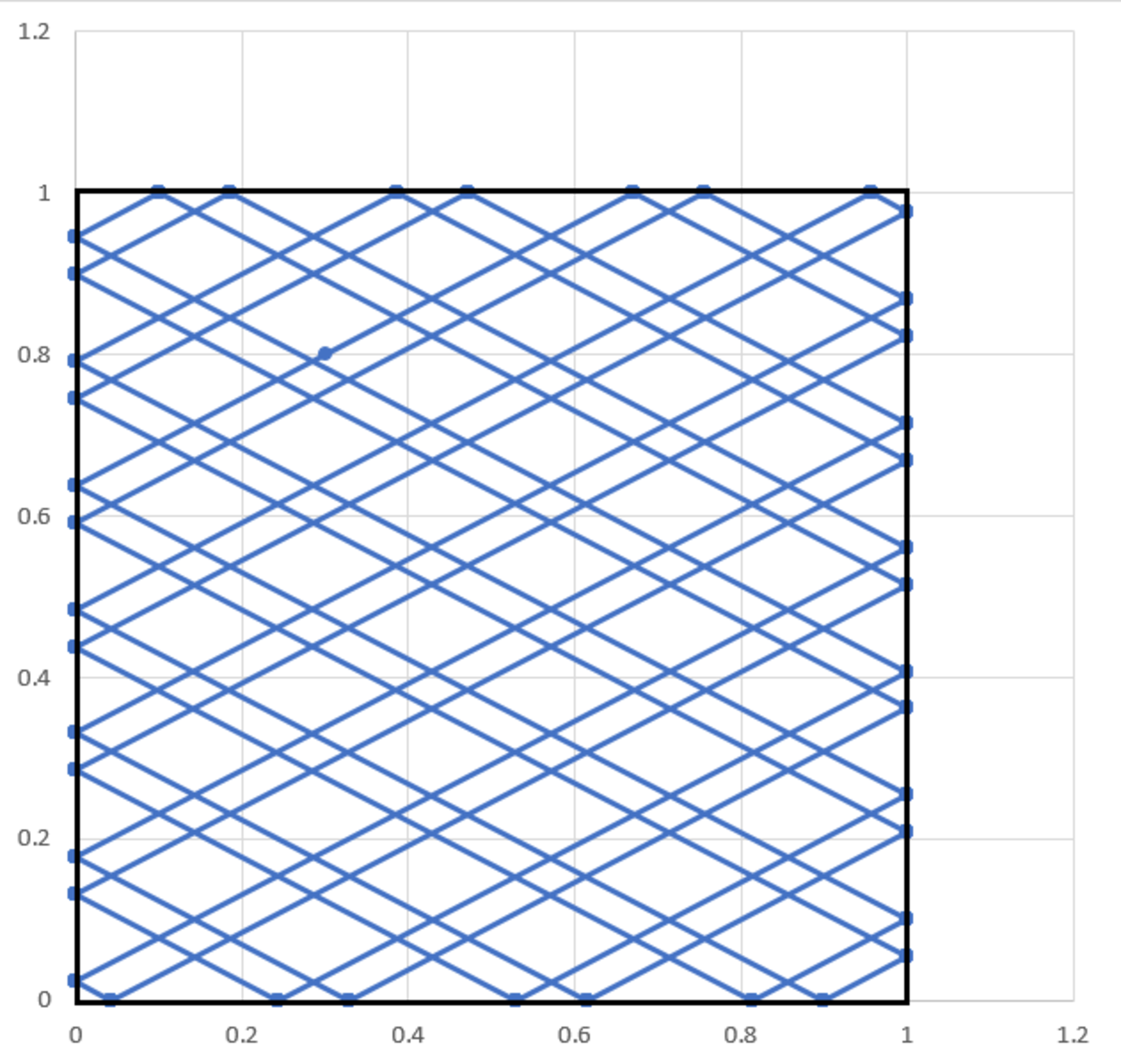
The answer is 0.63846.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!