Bouncy balls put on top of each other
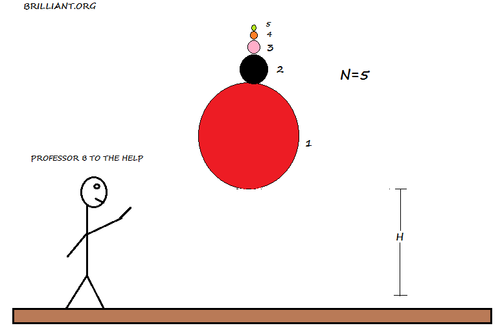 Bouncy balls are stacked on top of each other with decreasing mass as shown In the figure above. They are configured such that the one on the bottom is at a height of
above the ground. The figure above shown for
, but we can increase the number of ball to our liking.
Bouncy balls are stacked on top of each other with decreasing mass as shown In the figure above. They are configured such that the one on the bottom is at a height of
above the ground. The figure above shown for
, but we can increase the number of ball to our liking.
After the balls are released, and the first ball touches the ground, each ball bounces off its neighboring ball. If is the speed of the ball right after it bounces of its adjacent ball. What is the ratio of the speed of the ball right after it bounces to the ball right after it bounces.
Simply put what is
Details and assumptions
All the collisions that take place are elastic collisions.
Assume .
The answer is 33825.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since all collisions between balls are elastic, the coefficient of restitution is 1 . This means v s e p = v a p p , where v a p p is the velocity of approach between two adjacent balls just before collision and v s e p is the velocity of separation between those two balls just after collision.
Let's assume upward direction as positive and downward as negative.
Just before ball 1 collides with the ground, all the balls will have the same velocity. Let this velocity be v 0 downwards, that is − v 0 . Just after colliding with the ground, velocity of ball 1 will become v 0 upwards, that is + v 0 . Let's call it v 1 .
Now, ball 1 will collide with ball 2. We know that velocity of ball 2 is − v 0 just before collision. Also, velocity of ball 1 is v 1 just before collision. Since M 1 ≫ M 2 , we can assume velocity of ball 1 won't change at all, and the only change in velocity will be observed in ball 2, which has much less mass than ball 1. Therefore, velocity of ball 1 will remain v 1 just after collision as well. It's given that the velocity of ball 2 after collision is v 2 . The collision is again elastic, so we can still use v s e p = v a p p ,
v a p p = v 1 − ( − v 0 )
v s e p = v 2 − v 1
From the above equation we get
v 2 − v 1 = v 1 + v 0 ⟹ v 2 = 2 v 1 + v 0
By observing further, by induction, we get the following equation for v n for n ≥ 1
v n = 2 v n − 1 + v 0
But, we know v 1 = v 0 . For n = 2 , we get v 2 = 2 v 0 + v 0 = 3 v 0 . For n = 3 , v 3 = 6 v 0 + v 0 = 7 v 0
So, again, by observation we get a simplified general equation for v n , that is
v n = ( 2 n − 1 ) v 0
Now, we simply put n = 2 0 and n = 5 to get
v 5 v 2 0 = ( 2 5 − 1 ) v 0 ( 2 2 0 − 1 ) v 0
v 5 v 2 0 = 3 1 1 0 4 8 5 7 5
Finally we get v 5 v 2 0 = 3 3 8 2 5