Bouncy Bouncing Ball!
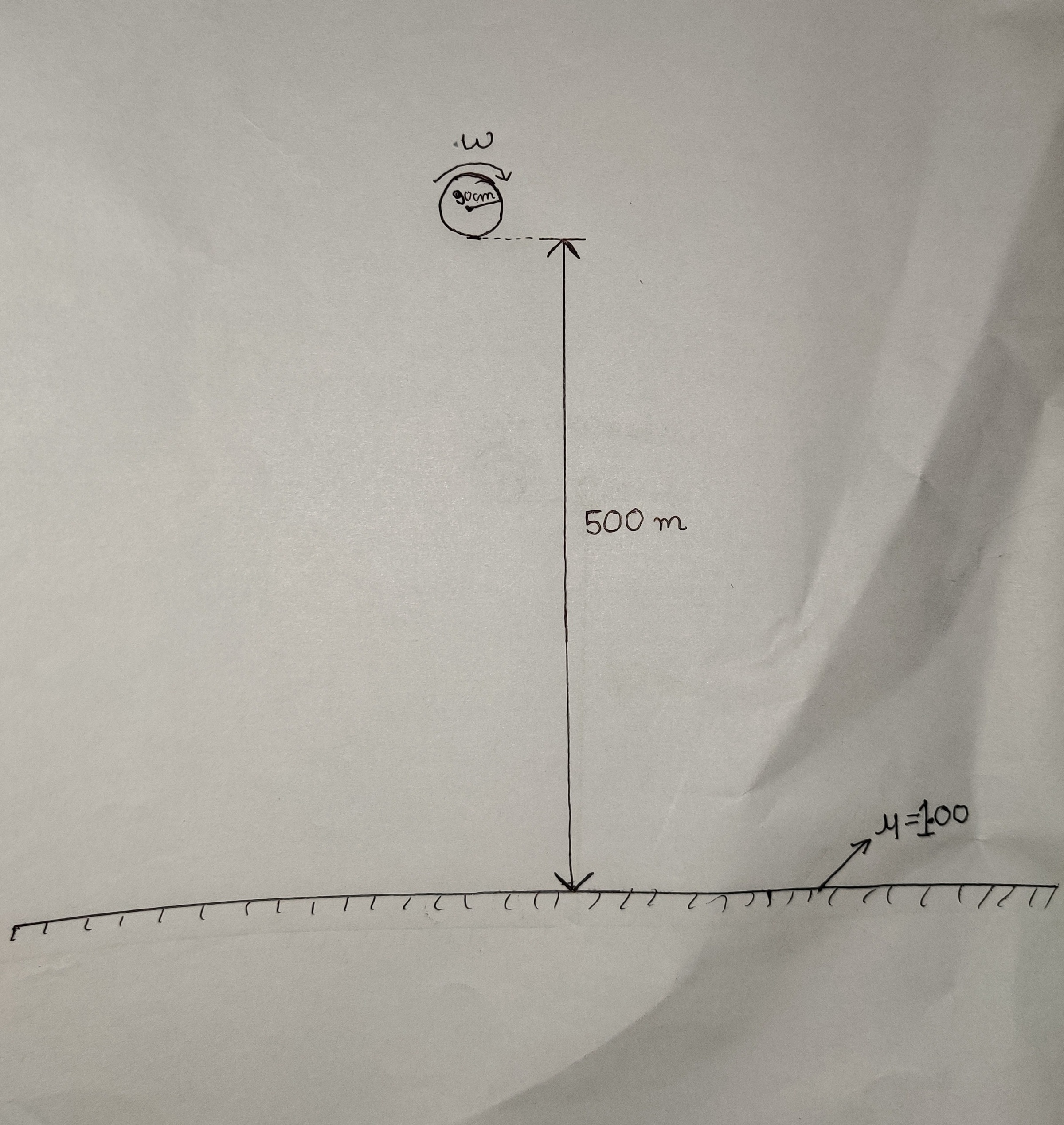
From a height h = 5 0 0 m , a uniform solid disc of radius R = 9 0 cm is given an angular velocity ω = 3 5 0 0 0 rad/s and dropped. The ground is rough and has coefficient of friction μ = 1 . After each collision, the disc's vertical speed becomes half ( 5 0 % ) of the value just before collision. If when the vertical velocity just becomes zero, the horizontal distance travelled by disc is r ( in m ) and the angular velocity of disc is ω ′ ( in rad / s ) , enter answer as r + ω ′ .
Take acceleration due to gravity g = 1 0 m/s 2 .
Inspiration Aniket Sanghi
All of my problems are original .
The answer is 5000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution:), but you need to fix some of the Latex in the first and second lines.
Log in to reply
Glad you liked the solution. :) Thanku for the correction.
It should be stated in the problem that the gravitational acceleration is 1 0 .
A few basic principles behind this problem:
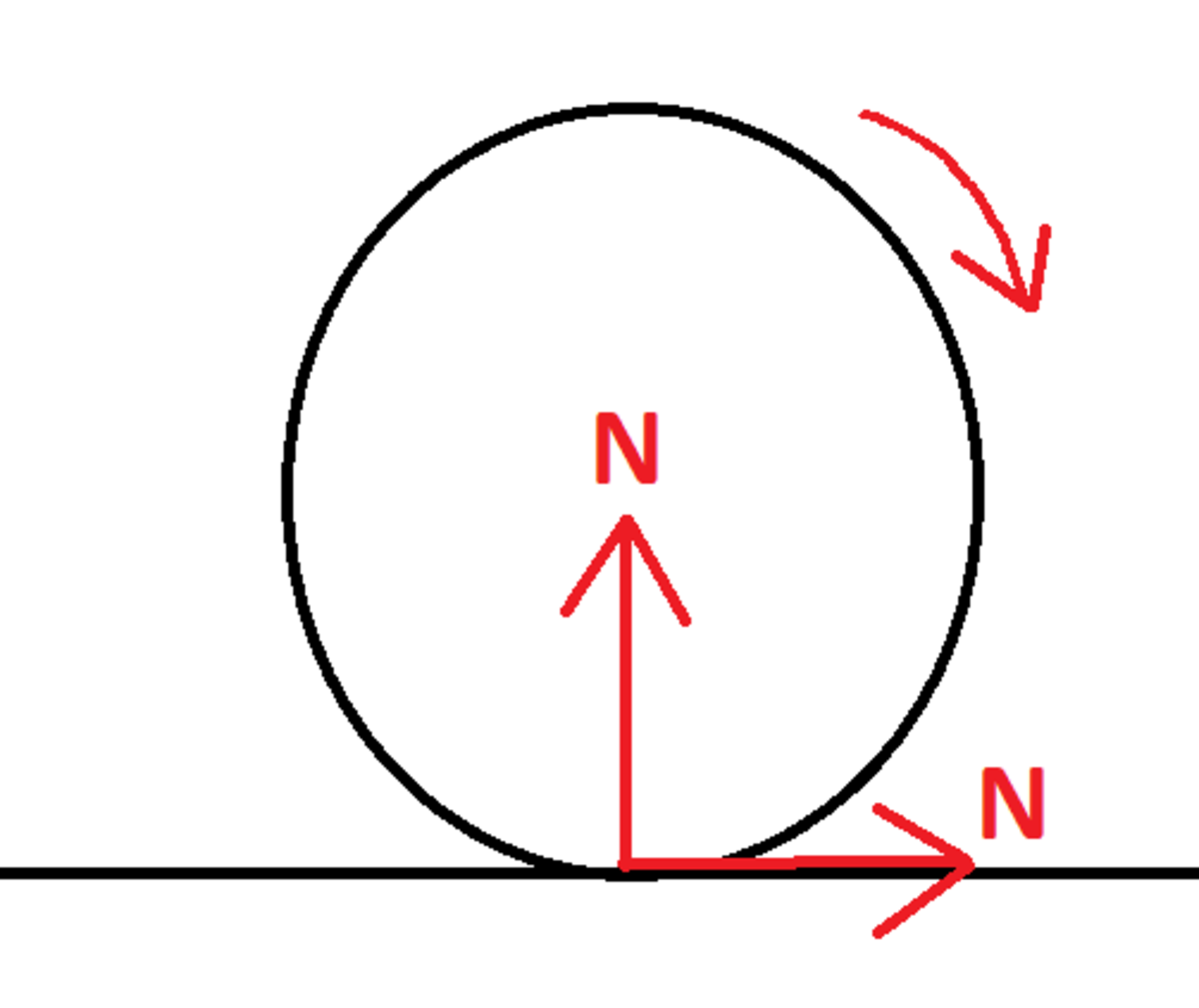
1) When the ball bounces, there is a vertical impulse and associated upward normal force. This causes the vertical speed after the bounce to be half of its value before the bounce. In order for this to happen, the magnitude of the impulse must be 1 . 5 times the vertical momentum right before the bounce (because the force has to get rid of all the downward speed before imparting half as much speed upward).
2) Because the friction coefficient is unity, the horizontal impulse is equal to the vertical impulse. This means that for each bounce, the horizontal speed increases by 1 . 5 times the vertical speed right before the bounce.
3) The horizontal friction force also reduces the angular speed. The relationships between translational and rotational quantities are given below ( I is the disk moment of inertia):
N Δ t = m Δ v x τ Δ t = − I Δ ω = N R Δ t = m R Δ v x Δ ω = − I m R Δ v x
Thus, the change in angular momentum for the bounce can be calculated once the change in horizontal speed is known. The attached code calculates the parameters right after the first bounce. It then simulates a large number of bounces to get limiting values for the horizontal distance traveled and the angular speed. These are:
x f = 4 0 0 0 ω f = 1 0 0 0
I'm sure it would also be possible to evaluate some geometric series analytically, as an alternative to the numerical approach.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
|
Excellent solution sir. Thanku for sharing it with us. :)
Log in to reply
Thanks. It was a fun problem
Let e = 0 . 5
Now, just before n t h bounce, the vertical velocity of ball will be e n − 1 v and just after n t h bounce, vertical velocity of ball would be e n v .
Also, let just after n t h bounce, let angular velocity be ω n and horizontal velocity be v n
Applying Impulse - momentum theorem, considering normal reaction N
∫ N d t = m ( e n v + e n − 1 v ) μ ∫ N d t = m ( v n − v n − 1 )
By above two equations
μ v ( e + 1 ) e n − 1 = v n − v n − 1
Solving above series, we get
μ v 1 − e 1 + e ( 1 − e n ) = v n
Apply Angular impulse - angular momentum theorem
μ R ∫ N d t = 2 m R 2 ( ω n − 1 − ω n )
Putting value of ∫ N d t from first equation
R 2 μ v ( 1 + e ) e n − 1 = ω n − 1 − ω n
Solving above series, we get
R 2 μ v 1 − e 1 + e ( 1 − e n ) = ω − ω n
Now, checking ω n R ≤ v n , we see it not true for any value of n for given values , so friction will act at every bounce in motion.
Putting n = ∞ and other values in question, we get
ω ′ = 1 0 0 0
Now, let range after n t h and before ( n + 1 ) t h bounce be r n
r n = g 2 v x v y r n = g 2 μ v 1 − e 1 + e ( 1 − e n ) e n v r n = g 2 μ v 2 1 − e 1 + e ( e n − e 2 n ) n = 0 ∑ ∞ r n = n = 0 ∑ ∞ g 2 μ v 2 1 − e 1 + e ( e n − e 2 n )
r = g 2 μ v 2 ( 1 − e ) 2 e
Putting values, we get
r = 4 0 0 0
ω ′ + r = 1 0 0 0 + 4 0 0 0 = 5 0 0 0