Boundary-phobia
The figure shows a blue region consisting of all points inside a unit square that are closer to the center than to the boundary of the square.
Find the area of the region.
The answer is of the form 3 A B − C , where A , B , C are positive integers with B square-free.
Enter your answer as A + B + C .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Jared Canright I too solved similarly, but for computing the integral you can use Weirstrass Substitution........That's easier to evaluate manually......
Log in to reply
I'm not familiar with that technique. I honestly haven't done Calc II since Calc II class. I'm in physics, where the attitude of "I've set up the integral that gives the solution; the computer can do the grunt work" is the prevailing attitude. I'd be interested to see how you carried out the integral.
Log in to reply
Well, I am not good with LATEX......So, I can send you a link.......https://en.wikipedia.org/wiki/Tangent half-angle substitution......This Substitution uses the half angle tangents and is pretty easy in evaluating integrals.......Hope you find it useful even without me explaining it.......!!
For any point in the triangle O A B , the nearest point on the boundary of the square to that point lies on the line A B Thus the curve C E D which marks the boundary of the desired region in the triangle O A B is the locus of points in O A B that are equidistant from O and A B ,
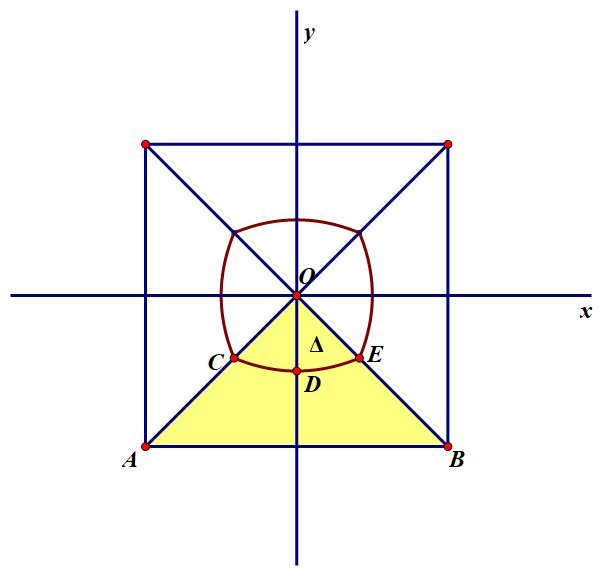
Thus the curve C D E is the intersection with O A B of the parabola that has focus O and directrix A B . Setting up a coordinate system with O at the origin, this parabola has equation y = x 2 − 4 1 . If Δ is the area of the sector O D E , then Δ = ∫ 0 2 1 ( 2 − 1 ) [ − x − ( x 2 − 4 1 ) ] d x = 2 4 1 ( 4 2 − 5 ) and so the desired area is 8 Δ = 3 1 ( 4 2 − 5 ) making the answer 4 + 2 + 5 = 1 1 .
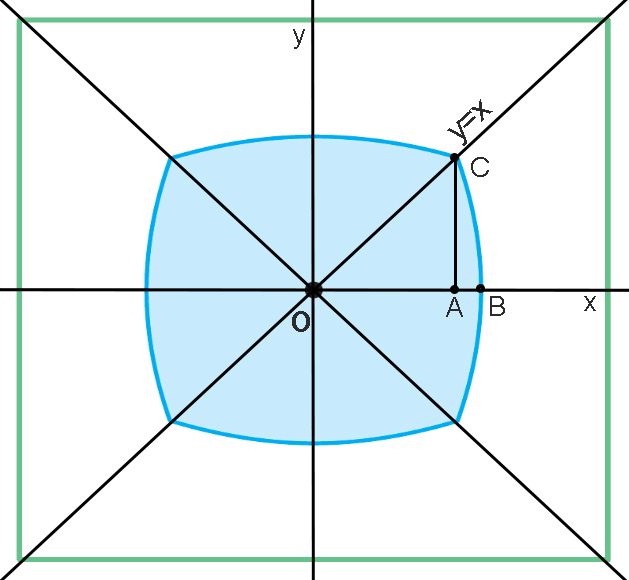
Let's be the origin O in the x y -plane the square center. Let be
P = { ( x , y ) ∈ R 2 ∣ − 2 1 ≤ x ≤ 2 1 , − 2 1 ≤ y ≤ 2 1 }
a generic point inside the square. The area A of the blue region is
A = ( 2 A C ) 2 + 8 ⋅ A r e a ( A B C )
because the ( 2 A C ) 2 square is 'surrounded' by 8 A B C small triangoloids.
Now, let's find the locus of point such that the distance of P from O is equal to the distance of P from the left vertical side of the unit square. That is
x 2 + y 2 = 2 1 − x ⟹ y = 4 1 − x
considering only the positive solution respect to y . This curve follows exactly the shape of the curved-edge BC ⌢ , although we need to find its boundaries. In order to do so, we intersect y = 4 1 − x with y = x to find the x -coordinate of A and C and with y = 0 to find the x -coordinate of B .
{ y = 4 1 − x y = x ⟹ x = A x = 2 2 − 1
considering only the positive solution of x .
{ y = 4 1 − x y = 0 ⟹ x = B x = 4 1
Now we are able to evaluate A
A = ( 2 A C ) 2 + 8 ∫ A x B x 4 1 − x d x = ( 2 ⋅ 2 2 − 1 ) 2 + 8 ∫ 4 1 2 2 − 1 4 1 − x d x = 3 4 2 − 5
Eventually A + B + C = 2 + 5 + 4 = 1 1
Notation: Let x and y be the usual horizontal and vertical Cartesian variables. We will make use of the polar coordinate system as well, using radius r = x 2 + y 2 and angle θ = tan ( x y ) .
Convention: Here, we use the convention that θ = 0 on the positive x -axis and increases counter-clockwise. We center the square at the origin (the black dot is at x=0, y=0). Since the box is of side length 1, we are limited to the domains − 2 1 ≤ x ≤ 2 1 and − 2 1 ≤ y ≤ 2 1 .
Strategy: Let's start by figuring out how to be lazy. This problem has a lot of symmetry we can exploit; in fact, we can break it up into 8 identical wedges of angle π / 4 . Knowing this, we can focus on finding the area of that single wedge and multiply our result by 8 at the end to get our final answer. Let's work with the wedge atop the positive x-axis, for which 0 ≤ θ ≤ 4 π .
Now, how do we find the area of this wedge? We could integrate along x and y , bounded by the x-axis, the line x=y, and the curve from the top right corner to the x -axis. This is unappealing; setting up an integral with a piecewise upper bound (part of which we do not yet know) would be ugly. Let's consider polar coordinates instead. We know from our earlier argument we need only integrate along 0 ≤ θ ≤ 4 π . If we can find a function for r (which seems inescapable either way), we can just plug it in and integrate over area.
Step 1 - Find constraints on r : Pick a point on the outer edge of the wedge. By premise, the distance r from the origin to this point is equal to the distance from this point to the nearest edge. Here the nearest edge is located at at x = 1 / 2 , so the distance from the edge to the point is 1 / 2 − x . Thus r = 1 / 2 − x .
Step 2 - Construct r ( θ ) : Recall that x = r cos θ ; plugging this into our equation from Step 1 gives r = 1 / 2 − r cos θ , which we can rearrange to find r ( θ ) = 2 1 1 + cos θ 1 .
Step 3 - Integrate over the wedge: Recall that a line drawn from the origin to a point ( r , θ ) moved by a very small increment δ θ covers area δ A = π r 2 2 π δ θ . Integrating this over the wedge gives us our area:
A w e d g e = ∫ 0 π / 4 π r 2 2 π d θ = 2 1 ∫ 0 π / 4 4 1 ( 1 + cos θ ) 2 1 d θ = 8 1 3 1 ( 4 2 − 5 ) .
Mathematica was used to compute the integral.
Step 4 - Wrapping up: Multiplying by 8 gives us the area of the entire region: 8 A w e d g e = 3 4 2 − 5 . We can read out and sum the top three numbers to arrive at our solution: 4 + 2 + 5 = 1 1 .