Tightly Bounded Area
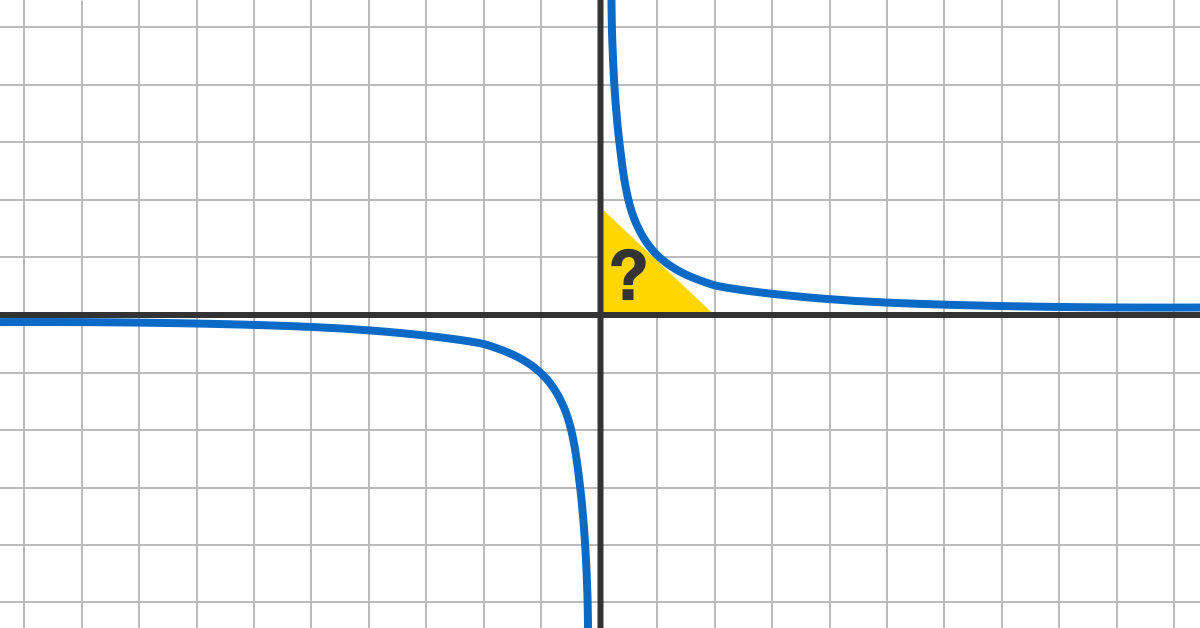
A tangent to the function is drawn on the first quadrant of the Cartesian plane.
Let denote the area bounded by this tangent, the -axis and the -axis.
What is the range of the values of can take?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the tangent touches f ( x ) at ( a , a 1 ) .
The gradient of the tangent is d x d f ( x ) ∣ ∣ ∣ ∣ x = a = d x d ( x 1 ) ∣ ∣ ∣ ∣ x = a = − a 2 1 .
The equation of the tangent is given by:
x − a y − a 1 ⟹ y = − a 2 1 = a 2 a − x = a 2 2 a − x
Let x − and y -axis intercepts be x 0 and y 0 respectively. Then we have:
0 ⟹ x 0 y 0 ⟹ y 0 = a 2 2 a − x 0 = 2 a = a 2 2 a − 0 = a 2
Then we have X = 2 1 x 0 y 0 = 2 1 ⋅ 2 a ⋅ a 2 = 2 , which is independent of a .