Bounded Balls
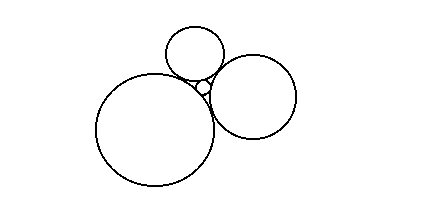 Four balls in the sketch above are all mutually tangent to one another. If the radii of the three larger balls are
69
,
46
, and
23
, what is the radius of the fourth ball?
Four balls in the sketch above are all mutually tangent to one another. If the radii of the three larger balls are
69
,
46
, and
23
, what is the radius of the fourth ball?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
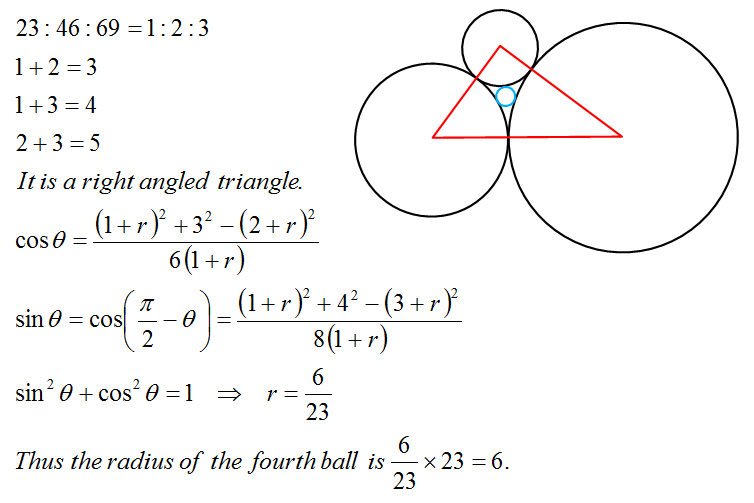
This involves an application of Descartes' theorem . From equation (2) in the link, noting that the curvature k of a circle of radius r is given by k = r 1 , and taking the positive root to find the curvature k 4 of the inscribed circle, we have that
k 4 = 6 9 1 + 4 6 1 + 2 3 1 + 2 6 9 ∗ 4 6 1 + 6 9 ∗ 2 3 1 + 4 6 ∗ 2 3 1 =
2 3 1 ∗ ( 3 1 + 2 1 + 1 ) + 2 3 2 6 1 + 3 1 + 2 1 = 2 3 1 ∗ 6 1 1 + 2 3 2 = 2 3 1 ∗ 6 2 3 = 6 1 .
Thus the radius of the fourth ball is k 4 1 = 6 .