Bounded by two paraboloids (Corrected)
Find the volume bounded by the two paraboloids,
and
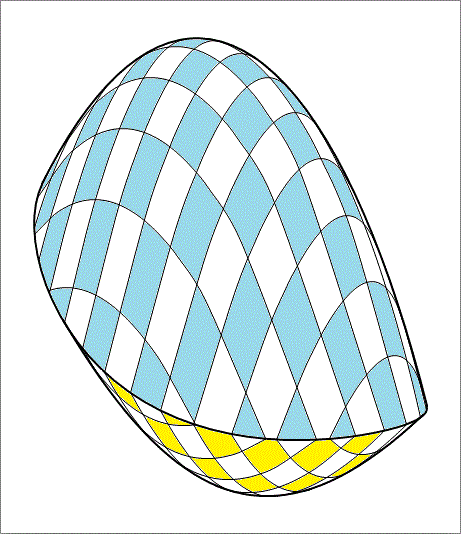
The answer is 2347.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We have,
z 1 = 2 0 − 0 . 1 x 2 − 0 . 2 ( y − 5 ) 2 = 2 0 − 0 . 1 x 2 − 0 . 2 y 2 + 2 y − 5 = 1 5 − 0 . 1 x 2 − 0 . 2 y 2 + 2 y
z 2 = . 1 ( x − 4 ) 2 + . 1 ( y − 6 ) 2 = 0 . 1 x 2 + 0 . 1 y 2 − 0 . 8 x − 1 . 2 y + 5 . 2
we have to find the intersection of this two surfaces, so equating the right hand sides of the above equations, gives the equation of projection of the curve of intersection onto the x y plane
1 5 − 0 . 1 x 2 − 0 . 2 y 2 + 2 y = 0 . 1 x 2 + 0 . 1 y 2 − 0 . 8 x − 1 . 2 y + 5 . 2
0 . 2 x 2 + 0 . 3 y 2 − 0 . 8 x − 3 . 2 y − 9 . 8 = 0
which is an equation of an ellipse.
Completing the squares for x and y , we obtain
0 . 2 ( x − 2 ) 2 − 0 . 8 + 0 . 3 ( y − 1 6 / 3 ) 2 − 1 6 2 / 3 0 − 9 . 8 = 0
Multiply by 10 throughout
2 ( x − 2 ) 2 + 3 ( y − 1 6 / 3 ) 2 = 9 8 + 1 6 2 / 3 + 8 = 5 7 4 / 3
Normalize the right hand side
( x − 2 ) 2 / ( 5 7 4 / 6 ) + ( y − 1 6 / 3 ) 2 / ( 5 7 4 / 9 ) = 1
Let a 2 = 5 7 4 / 6 and b 2 = 5 7 4 / 9
then parametrically, points inside the ellipse can be written as
x = 2 + a r cos t , y = 1 6 / 3 + b r sin t
where t ∈ [ 0 , 2 π ] and r ∈ [ 0 , 1 ] .
now we'll integrate the difference between the z-values of the two paraboloids over the area bounded by the ellipse, this can be achieved by the following double integral
V = ∫ A ( z 1 − z 2 ) d A = ∬ A ( z 1 ( x , y ) − z 2 ( x , y ) ) d x d y
From the expressions obtained above, this becomes,
V = ∬ A − ( 0 . 2 x 2 + 0 . 3 y 2 − 0 . 8 x − 3 . 2 y − 9 . 8 ) d x d y
Plugging the expressions for x and y into the integrand, and using the jacobian of the transformation we made, we obtain,
V = a b ∫ r = 0 1 ∫ t = 0 2 π − ( 0 . 2 ( 2 + a r cos t ) 2 + 0 . 3 ( 1 6 / 3 + b r cos t ) 2 − 0 . 8 ( 2 + a r cos t ) − 3 . 2 ( 1 6 / 3 + b r sin t ) − 9 . 8 ) d t r d r
Integrating the above expressions with respect to t is a simple task. This is due to the fact that linear terms in cos t and sin t integrate to zero, and quadratic terms integrate to π times the coefficient of cos 2 ( t ) or sin 2 ( t ) . All the other constants will integrate to their value multiplied by 2 π .
Hence,
V = 2 a b π ∫ r = 0 1 ( − 0 . 8 − 0 . 3 ( 1 6 / 3 ) 2 + 1 . 6 + 3 . 2 ( 1 6 / 3 ) + 9 . 8 − 1 / 2 ( 0 . 2 a 2 r 2 + 0 . 3 b 2 r 2 ) r d r
Adding up the constant terms and the coefficient of r 2 , we obtain,
V = 2 a b π ∫ r = 0 1 ( 1 9 . 1 3 3 3 3 3 3 3 − ( 0 . 1 a 2 + 0 . 1 5 b 2 ) r 2 ) r d r
Now, integrating with respect to r , we obtain,
V = 2 a b π ( 2 1 ( 1 9 . 1 3 3 3 3 3 3 ) − 4 1 ( 0 . 1 a 2 + 0 . 1 5 b 2 ) )
Substituting a 2 = 5 7 4 / 6 , b 2 = 5 7 4 / 9 , we obtain the final value of V, namely,
V = 2 3 6 5 7 4 π ( 4 1 ) ( 1 9 . 1 3 3 3 3 3 3 3 ) ≈ 2 3 4 7 . 6