Bounding the Masses!
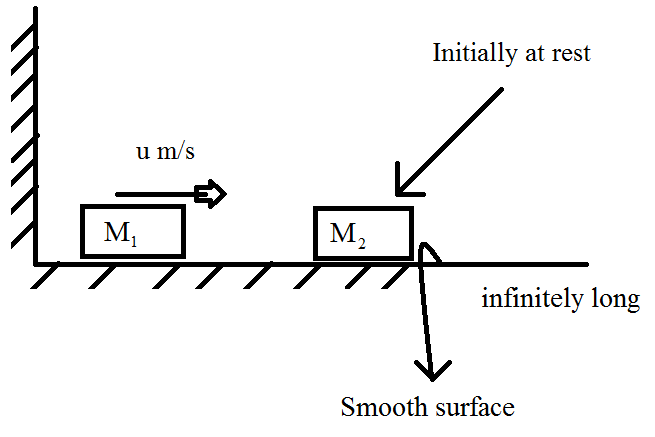
A block of mass is projected on a smooth floor towards another block of mass with a speed as shown in the figure.
If, for exactly 3 collisions to occur in this setup, the value of satisfies the inequality for real number masses and , then there exists a real number mass such that
Give your answer as where denotes the floor function .
Assume that all collisions are perfectly elastic (the coefficient of restitution, ).
Image Credit: Rishabh Deep Singh
The answer is 2773.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If the masses M 1 , M 2 have velocities u 1 , u 2 before a collision and velocities v 1 , v 2 after a collision, then M 1 v 1 + M 2 v 2 = M 1 u 1 + M 2 u 2 − v 1 + v 2 = u 1 − u 2 and hence v 1 = M 1 + M 2 ( M 1 − M 2 ) u 1 + 2 M 2 u 2 v 2 = M 1 + M 2 2 M 1 u 1 + ( M 2 − M 1 ) u 2 Thus, after the first collision of the masses, they have speeds M 1 + M 2 M 1 − M 2 u and M 1 + M 2 2 M 1 u respectively. For there to be a second collision, the M 1 mass must now hit the wall, and hence we must have M 1 < M 2 . After the collision of the M 1 mass with the wall, it now has velocity M 1 + M + 2 M 2 − M 1 u . Provided that M 2 − M 1 > 2 M 1 , the two masses will collide again. Thus we get at least three collisions provided that M 2 > 3 M 1 . After this third collision, the M 1 , M 2 masses have velocities ( M 1 + M 2 ) 2 6 M 1 M 2 − M 1 2 − M 2 2 u ( M 1 + M 2 ) 2 4 M 1 ( M 2 − M 1 ) u respectively. There will therefore be exactly three collisions provided that 0 ≤ 6 M 1 M 2 − M 1 2 − M 2 2 = 8 M 1 2 − ( M 2 − 3 M 1 ) 2 Putting this altogether, there will be exactly three collisions provided that 3 M 1 < M 2 ≤ ( 3 + 8 ) M 1 . Thus we require 3 π < Γ ≤ ( 3 + 8 ) π and hence γ = ( 6 + 8 ) π , which makes ⌊ 1 0 0 γ ⌋ = 2 7 7 3 .