Bouyant force
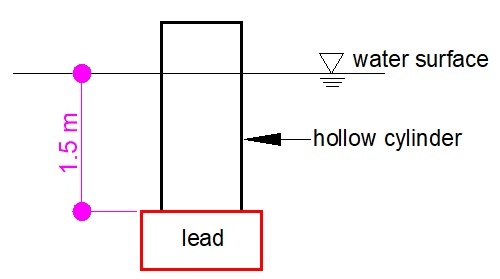 A hollow cylinder
m. in diameter and
m. long weighs
newtons. How many kilonewtons of lead weighing
kilonewtons per cubic meter must be fastened to the outside bottom to make the cylinder float vertically with
m. submerged in fresh water. Give your answer to one decimal place.
A hollow cylinder
m. in diameter and
m. long weighs
newtons. How many kilonewtons of lead weighing
kilonewtons per cubic meter must be fastened to the outside bottom to make the cylinder float vertically with
m. submerged in fresh water. Give your answer to one decimal place.
Details:
-
The unit weight of fresh water is kilonewtons per cubic meter.
-
“m” means meter
-
Use .
The answer is 8.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Fluid Mechanics
W C + W L = B F C + B F L
3 . 8 2 5 + W L = 4 π ( 1 ) 2 ( 1 . 5 ) ( 9 . 8 1 ) + V L ( 9 . 8 1 )
However, γ L = V L W L or V L = 1 1 0 W L
So we have
3 8 2 5 + W L = 4 3 . 1 4 1 6 ( 1 ) 2 ( 1 . 5 ) ( 9 . 8 1 ) + 1 0 0 W L ( 9 . 8 1 )
W L ≈ 8 . 5 k N
Symbols:
W L = weight of lead
W C = weight of cylinder
B F L = bouyant force of lead
B F C = bouyant force of cylinder
γ L = unit weight of lead
V L = volume of lead
W L = weight of lead
Note:
Bouyant Force = weight of the fluid displaced = volume of object displaced x unit weight of fluid