Bowling-Ball coins
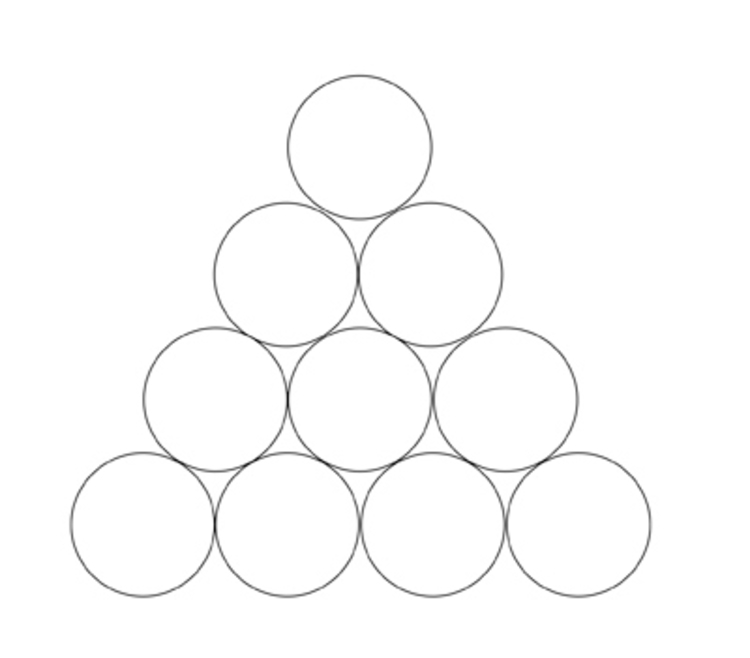Arrange ten coins as shown in the image above.What is the smallest number of coins that you must remove so that there is no equilateral triangle of any size which will have its three vertices marked by the centers of the three coins that remain?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
You didn't show that it's minimum. Read the hint I gave in Chew-Seong Cheong's solution.
In response to Challenge Master: @Calvin Lin @Brilliant Mathematics
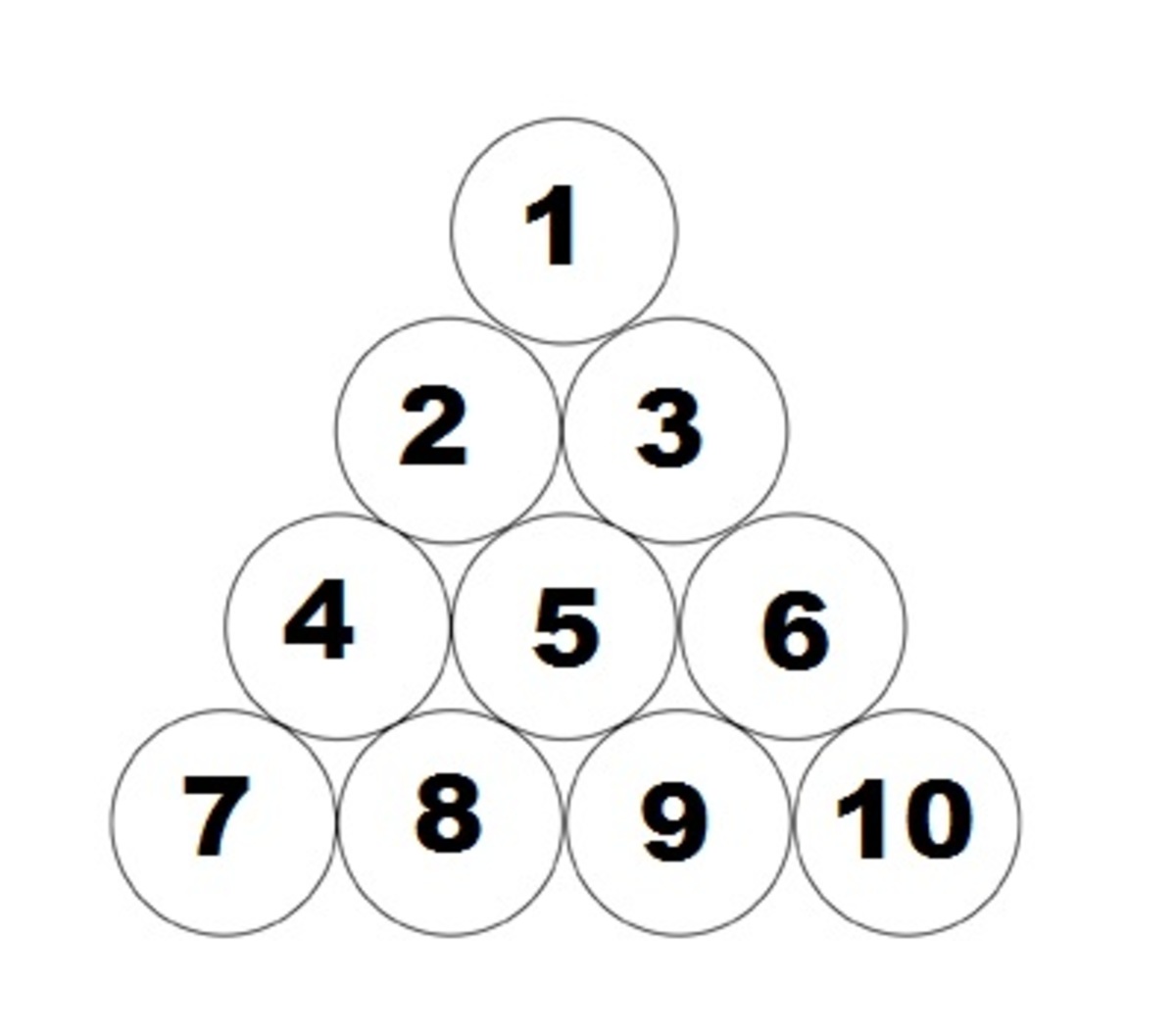
Lets number the coins 1 to 10 as shown in the image above.
-
We don't want the biggest equilateral triangle that is of vertices 1 , 7 , 1 0 to be formed. So we must eliminate one of 1 , 7 , 1 0 . So let's eliminate 1 .
-
Now we don't want the medium sized triangle(s) that have vertices ( 1 , 4 , 6 ) , ( 2 , 7 , 9 ) , ( 3 , 8 , 1 0 ) , ( 2 , 8 , 6 ) , ( 3 , 4 , 9 ) . Since 1 is already eliminated , ( 1 , 4 , 6 ) cannot be formed. So if we eliminate the common points 8 , 9 , none of the remaining four triangles can be formed. So we eliminate 8 , 9 .
-
Now we want to get rid of smallest triangle(s) that have vertices ( 1 , 2 , 3 ) , ( 2 , 4 , 5 ) , ( 3 , 5 , 6 ) , ( 4 , 7 , 8 ) , ( 5 , 8 , 9 ) , ( 6 , 9 , 1 0 ) . Since 1 , 8 , 9 are already eliminated , ( 1 , 2 , 3 ) , ( 4 , 7 , 8 ) , ( 5 , 8 , 9 ) , ( 6 , 9 , 1 0 ) cannot be formed. So now we need to eliminate ( 2 , 4 , 5 ) , ( 3 , 5 , 6 ) and we can do this by eliminating the common point that is 5 .
So we conclude that we eliminate 1 , 8 , 9 , 5 in order to remove minimum number of coins. Hence its proved that the answer is indeed 4 .
Sorry, this solution is unvalid. There are two equilateral triangles within.
My solution is symmetrical.
Moderator note:
This solution has been marked wrong.
Can you prove that it's minimum?
Hint : First consider if there can't a largest equilateral triangle, which circle should be eliminated first? What should I do next?
Although the answer is 4 , I think that there are two equilateral triangles that can be formed from this particular configuration.
Log in to reply
I agree , there are 2 equilateral triangles that can be formed in @Chew-Seong Cheong sir's solution.
In your solution , the triangles ( 2 , 8 , 6 ) , ( 3 , 4 , 9 ) can still be formed. Hence , your solution is flawed.
In the figure provided there are 3 levels and sizes of equilateral triangles that are very clear and visible and another 4th size included in the hexagon
With a total number of 15 triangle; so to violate all these triangle together we have to remove the most common vertices
Now we should also remove the coin in the center as it's common in 6 triangles
Now to eliminate the 2 triangle with the hexagon we must eliminate 2 of the hex coins, so we should pick the 2 most common coins in that case they should be the last row's mid coins as they are common in 4 distinct triangles other than the ones with the hex, 2 of size 1 and 2 of size 2
up to this step we already removed 12 triangles, 3 more to go
we eliminate those 3 final common head 3 sizes be removing their common head which is the top coin
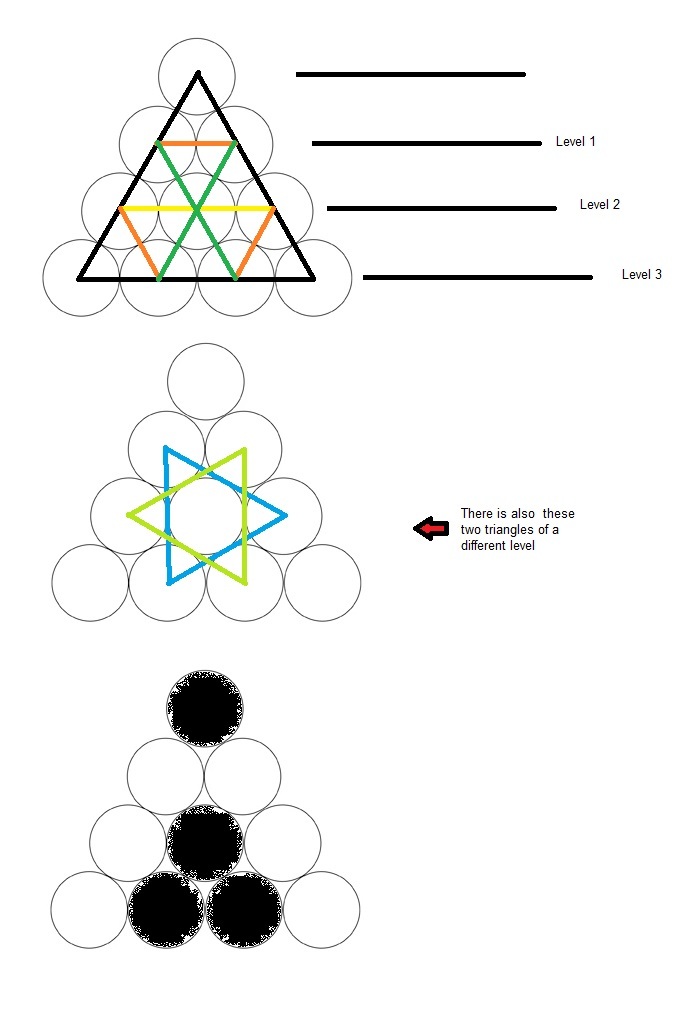
We can remove the minimum number of coins that are marked red in the image above such that there is no equilateral triangle of any size which will have its three vertices marked by the centers of the three coins that remain. Hence , the answer is 4 .