Box in the Air (Part 2)

Geometry Level 2

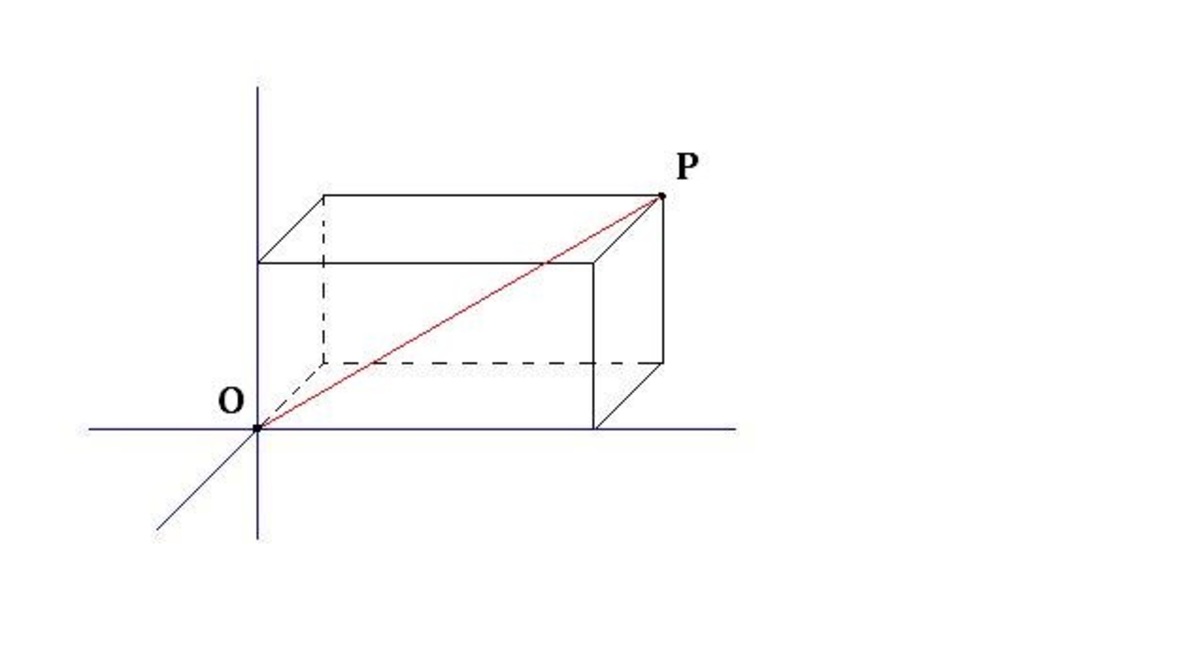
The point $O$ is the origin in the $xyz$ coordinates, and the point $P$ is the vertex of a cuboid, as shown above. The length of $OP$ is 7 while the three dimensions are all integers, where the length is the product of the width and the height of the cuboid.

What is the volume of the cuboid?

The answer is 36.

1 solution

Worranat Pakornrat
Mar 5, 2016

Let $x$ , $y$ , & $z$ be the length, width, and height of the cuboid respectively.

Then $x^2 + y^2 + z^2 = 7^2$

$(yz)^2 + y^2 + z^2 = 49$

$(y^2)(z^2 + 1) + z^2 = 49$

$(y^2) = \dfrac{49 - z^2}{z^2 + 1}$

Now since $z$ must be an integer less than 7, its value can vary from $1$ to $6$ :

If $z = 1$ , then $y^2 = 24$ .

If $z = 2$ , then $y^2 = 9 ; y = 3$ .

If $z = 3$ , then $y^2 = 4 ; y = 2$ .

If $z = 4$ , then $y^2 = \dfrac{33}{17}$ .

If $z = 5$ , then $y^2 = \dfrac{12}{13}$ .

If $z = 6$ , then $y^2 = \dfrac{13}{37}$ .

Therefore, $x = yz = 6$ , and so the volume of the cuboid = $xyz = x^2 = \boxed{36}$ .

Moderator note:

That's a nice problem.

Note that the condition of "length is the product of the width and the height of the cuboid" isn't necessary, as the volume of the cuboid will be the same regardless of what order the sides are in.

Oh, thank you for the review. Maybe I'll ask about the longest side next time.

Worranat Pakornrat - 5 years, 3 months ago

Box in the Air (Part 2)

The answer is 36.

1 solution

Moderator note:

0 pending reports