Box on Two Surfaces (Part 3)

Classical Mechanics Level 3

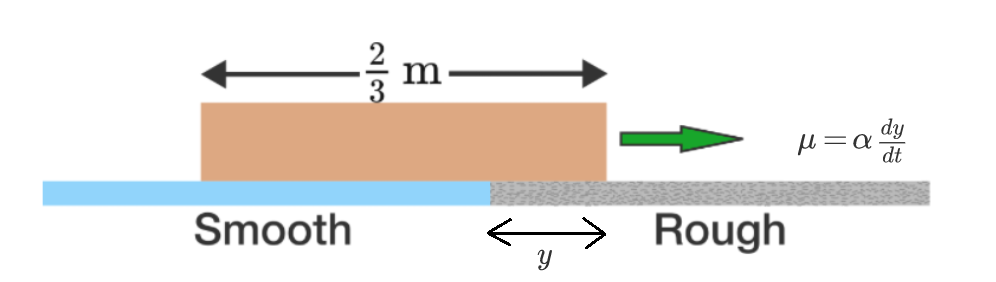
A rectangular box of length $\frac{2}{3} \text{m}$ is initially traveling at $3 \text{ m/s},$ with its entire length over the smooth (perfectly frictionless) blue surface (shown above). The box gradually moves onto a rough surface (gray) and stops the instant that its entire length is positioned within the rough region.

Call the overlap distance of the box into the rough region $y$ . The coefficient of friction within the rough region varies according to ( $\mu = \alpha \frac{dy}{dt}$ ) (see details and assumptions).

Determine the value of $\alpha$ .

Details and Assumptions:

$g = 10\text{ m/s}^2.$
The pressure at the bottom of the box is always uniform over its area.
Note that the friction coefficient is uniform over space within the rough region. But at any point in space, the friction coefficient varies over time in response to the box's changing position.
Thanks to Md Zuhair for the inspiration for this problem

The answer is 0.9.

1 solution

Md Zuhair
Nov 12, 2017

Hm, I didnt knew i made such a good question :).

Well lets start solving it.

Mass on the rough space= $\dfrac{My}{L}$ .

So friction= $\dfrac{Mgy \mu}{L}$

Now this friction causes acceleration for the whole body, so

$M \times a_{body}= \dfrac{Mgy \mu}{L}$

$\implies a_{body}= \dfrac{ gy \mu}{L}$

$\implies \dfrac{dv}{dt} = \dfrac{ gy \alpha dy}{L.dt}$

$\implies dv= \dfrac{gy \alpha dy}{L}$

Now integrating for $v=0$ to $v=3 m/s$ with simultaneous y being, $y = 0 \rightarrow \dfrac{2}{3}$

Solving the equation, we get

$\alpha = \boxed{0.9}$

Box on Two Surfaces (Part 3)

The answer is 0.9.

1 solution

0 pending reports