Boxes Out, Segments In
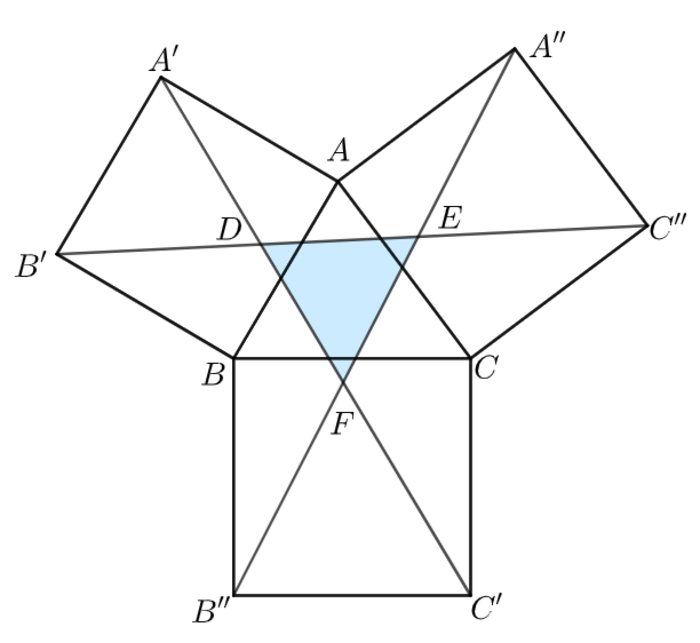
As shown above, three squares are extended from their respective vertices of of side lengths , and . Six segments are then extended to form shaded in blue.
If its area can be expressed as , where and are positive integers and , input as your answer.
The answer is 28855.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Place the diagram on the coordinate plane so that B is at B ( 0 , 0 ) and C is at C ( 1 4 , 0 ) .
The 1 3 - 1 4 - 1 5 triangle is a 5 - 1 2 - 1 3 right triangle combined with a 9 - 1 2 - 1 5 right triangle, so the coordinates of A are A ( 5 , 1 2 ) .
To go from B to A you go 5 right and then 1 2 up, so to go from A to A ′ you go 1 2 left and 5 up (since ∠ B A A ′ is a right angle), so the coordinates of A ′ are A ′ ( 5 − 1 2 , 1 2 + 5 ) = A ′ ( − 7 , 1 7 ) .
In a similar manner, you can calculate the coordinates B ′ ( − 1 2 , 5 ) , B ′ ′ ( 0 , − 1 4 ) , C ′ ( 1 4 , − 1 4 ) , A ′ ′ ( 1 7 , 2 1 ) , and C ′ ′ ( 2 6 , 9 ) .
Then the line through B ′ ( − 1 2 , 5 ) and C ′ ′ ( 2 6 , 9 ) follows y = 1 9 2 ( x − 2 6 ) + 9 , the line through A ′ ( − 7 , 1 7 ) and C ′ ( 1 4 , − 1 4 ) follows y = − 2 1 3 1 ( x + 7 ) + 1 7 , and the line through B ′ ′ ( 0 , − 1 4 ) and A ′ ′ ( 1 7 , 2 1 ) follows y = 1 7 3 5 x − 1 4 .
The intersection of y = 1 9 2 ( x − 2 6 ) + 9 and y = − 2 1 3 1 ( x + 7 ) + 1 7 is D ( 6 3 1 1 6 1 , 6 3 1 3 9 6 9 ) , the intersection of y = 1 9 2 ( x − 2 6 ) + 9 and y = 1 7 3 5 x − 1 4 is E ( 6 3 1 6 5 4 5 , 6 3 1 4 6 4 1 ) , and the intersection of y = − 2 1 3 1 ( x + 7 ) + 1 7 and y = 1 7 3 5 x − 1 4 is F ( 6 3 1 3 6 8 9 , − 6 3 1 1 2 3 9 ) .
Then F E = ( 6 3 1 2 8 5 6 , 6 3 1 5 8 8 0 ) and F D = ( − 6 3 1 3 5 2 8 , 6 3 1 5 2 0 8 ) , so the area of △ D E F = 2 1 ∣ ∣ ∣ ∣ 6 3 1 2 8 5 6 − 6 3 1 3 5 2 8 6 3 1 5 8 8 0 6 3 1 5 2 0 8 ∣ ∣ ∣ ∣ = 6 3 1 2 8 2 2 4 , so a = 2 8 2 2 4 , b = 6 3 1 , and a + b = 2 8 8 5 5 .