Boxed In
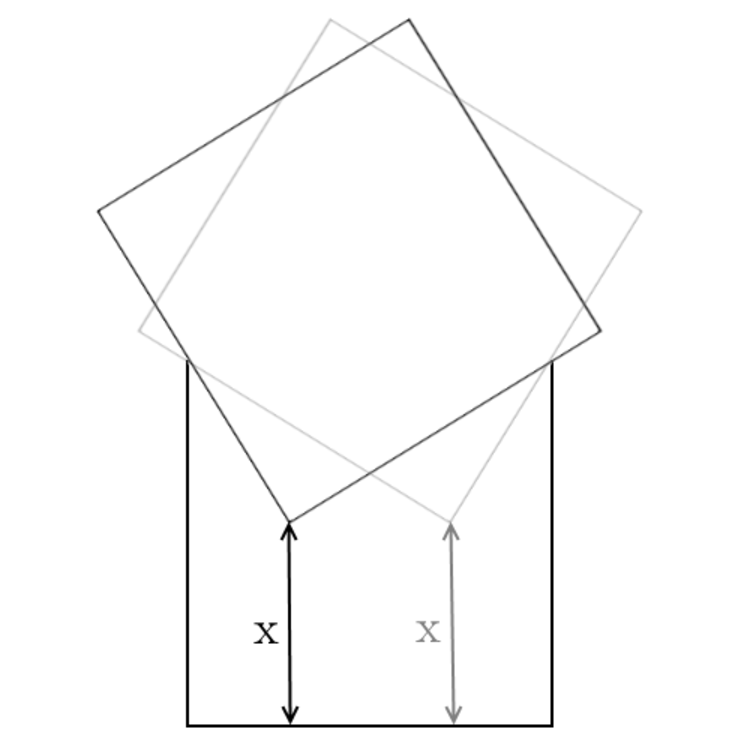 A square with side
falls on top of an open top square box with side
(pictured above). Assuming the square doesn't fall completely in the box, find the smallest value for
, where
is the the line that connects the vertex of the square inside the box to the box base perpendicularly.
A square with side
falls on top of an open top square box with side
(pictured above). Assuming the square doesn't fall completely in the box, find the smallest value for
, where
is the the line that connects the vertex of the square inside the box to the box base perpendicularly.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As the square falls on top of the box, a right angled triangle forms. The hypotenuse must be 1 , and the legs could be a variety of lengths. As we know, angles in a semicircle are 9 0 ° so the vertex of the triangle could lie anywhere on the semi-circle pictured above.
To find the smallest value for x , we must find the largest value for the depth of this triangle, and subtract that value from 1 . The maximum depth of the semicircle is its radius, which is of course half of the diameter ( 1 ).
x = 1 − 2 1 x = 2 1