Boxed parabolas
Two parabolas (in blue) intersect at two points. The four tangent lines (in red) at their points of intersection form a 3 × 4 rectangle. Find the area of the closed region created by both parabolas.
Find the area of the region bounded by the 2 curves.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
This is known as the Archimedes Triangle; he was the first to prove the theorem cited above.
The proof is fairly lengthly, although you can read it here . (Note: External link.)
The general idea is to break the "unfilled" portion of the parabola into triangles (as shown above); then break the remaining portion into more triangles; then break the remaining portion after that into more triangles, and so on.
This gets the infinite sum
2 1 ( 1 + 4 1 + ( 4 1 ) 2 + ( 4 1 ) 3 + ⋯ ) .
Using the infinite geometric series formula on the inside of the parentheses gets a value of 3 4 , so the entire expression comes out to be equal to 3 2 .
"Take two points on a parabola, and draw the tangents to the parabola at these points. Then the area of the parabolic segment is equal to 2/3 the area of the triangle formed by the two points and the intersection of the tangents." It may be true, but a proof of this lemma should have been provided! Good job, anyways!
Log in to reply
This link has a proof of the lemma: https://en.m.wikipedia.org/wiki/The Quadrature of the Parabola
Could you explain why it’s 2/3?
Log in to reply
I added a note with a brief summary and link to the proof.
This is a slightly different case. The triangle is created by chord and tangents rather than chord and a point on a parabola. Wikipedia article on Quadrature of the parabola
Log in to reply
Maria, you might be focusing on the intersection points of the original diagram (lower right and upper left); this solution focuses on the lower left and upper right corners which have the chords as shown.
The ratio of area of the triangle formed by 3 chords to that formed by drawing tangents at endpoints of the chords is 1/2 So the question is how did the area of the triangle you just shown is twice the area of the triangle formed by the the tangents and the chord?
Instead of finding a parabola to fit a box, I'm going to start with a parabola and put a box around it.
The parabola will be of the form x 2 = 4 a y , so that any point on the parabola can be expressed in the parametric form P = ( 2 a p , a p 2 ) where p is a parameter. From this, we know a bunch of important equations, which can be proven fairly easily:
- The equation of the chord between the points P ( 2 a p , a p 2 ) and Q ( 2 a q , a q 2 ) is y = 2 1 ( p + q ) x − a p q
- The equation of the tangent to the parabola at a point P is y = p x + a p 2
- The coordinates of the intersection of the tangents at points P and Q is T ( a ( p + q ) , a p q )
- If the chord PQ is a focal chord (i.e. passes through the point ( 0 , a ) ), then p q = − 1
- Combining the two statements above, if the chord PQ is a focal chord then the intersection of the tangents of P and Q is ( a ( p + q ) , − a )
Using this we can find values of
a
,
p
and
q
so that the tangents are of length 3 and 4 and meet at right angles. So we need to know the distance from each point on the parabola to the intersection of the tangents.
distance
=
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
P
T
P
T
=
(
2
a
p
−
a
(
p
+
q
)
)
2
+
(
a
p
2
+
a
)
2
=
a
2
(
p
−
q
)
2
+
a
2
(
p
2
+
1
)
2
=
a
(
p
−
q
)
2
+
(
p
2
+
1
)
2
=
a
(
p
+
p
1
)
2
+
(
p
2
+
1
)
2
=
a
p
2
1
(
p
2
+
1
)
2
+
(
p
2
+
1
)
2
=
a
(
p
2
+
1
)
2
(
p
2
1
+
1
)
Q
T
But
p
q
=
−
1
,
so
q
=
−
p
1
Q
T
=
(
2
a
q
−
a
(
p
+
q
)
)
2
+
(
a
q
2
+
a
)
2
=
a
2
(
q
−
p
)
2
+
a
2
(
q
2
+
1
)
2
=
a
(
q
−
p
)
2
+
(
q
2
+
1
)
2
=
a
(
−
p
1
−
p
)
2
+
(
p
2
1
+
1
)
2
=
a
p
2
(
p
2
1
+
1
)
2
+
(
p
2
1
+
1
)
2
=
a
(
p
2
+
1
)
(
p
2
1
+
1
)
2
Now we simply let PT=3 and QT=4 and solve simultaneously for
a
and
p
a
(
p
2
+
1
)
2
(
p
2
1
+
1
)
=
3
a
(
p
2
+
1
)
(
p
2
1
+
1
)
2
=
4
(
1
)
÷
(
2
)
(
1
)
(
2
)
(
p
2
+
1
)
(
p
2
1
+
1
)
2
(
p
2
+
1
)
2
(
p
2
1
+
1
)
(
p
2
1
+
1
)
(
p
2
+
1
)
(
1
+
p
2
)
p
2
(
p
2
+
1
)
p
2
p
=
4
3
=
1
6
9
=
1
6
9
=
1
6
9
=
4
3
↗
substitute
p
into
(
1
)
a
(
(
4
3
)
2
+
1
)
2
(
(
3
4
)
2
+
1
)
a
=
3
=
1
2
5
1
4
4
Now we can find the equation of both the parabola and the chord PQ, which we will need in a moment.
x
2
=
4
a
y
y
=
4
a
x
2
y
=
5
7
6
1
2
5
x
2
y
=
2
1
(
p
+
q
)
x
−
a
p
q
y
=
2
1
(
p
−
p
1
)
x
+
a
y
=
−
2
4
7
x
+
1
2
5
1
4
4
We can also get the x coordinates of the points P and Q, which we will use as the terminals of an integral to find the area.
x
1
=
2
a
p
=
1
2
5
2
1
6
x
2
=
2
a
q
=
−
p
2
a
=
−
1
2
5
3
8
4
Now we can finally put together an integral. The area we want is the curved shape shown here:
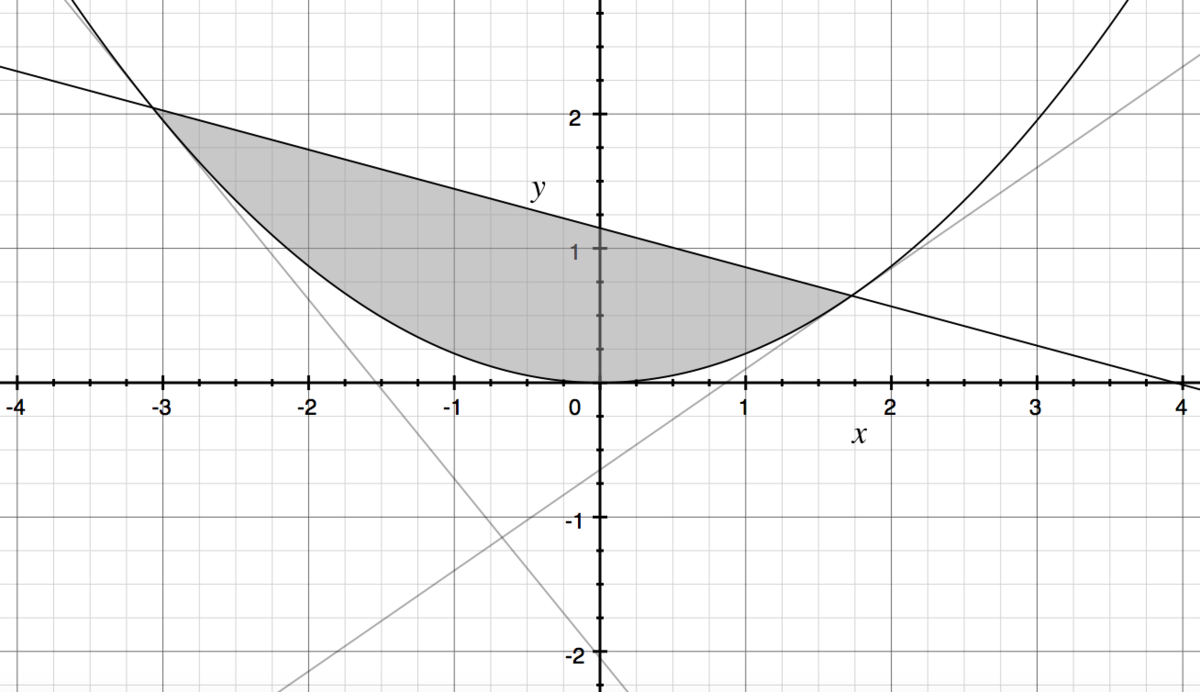 The integral will simply be the equation of the chord minus the equation of the parabola, between the two points we worked out above:
∫
−
1
2
5
3
8
4
1
2
5
2
1
6
(
−
2
4
7
x
+
1
2
5
1
4
4
−
5
7
6
1
2
5
x
2
)
d
x
=
4
This is easy to evaluate using the power rule, albeit with some annoying fractions, but you should end up with an answer of 4. This is only half the area we need though, as we get the shape above from cutting the rectangle along the diagonal, so the final answer will be
8
.
The integral will simply be the equation of the chord minus the equation of the parabola, between the two points we worked out above:
∫
−
1
2
5
3
8
4
1
2
5
2
1
6
(
−
2
4
7
x
+
1
2
5
1
4
4
−
5
7
6
1
2
5
x
2
)
d
x
=
4
This is easy to evaluate using the power rule, albeit with some annoying fractions, but you should end up with an answer of 4. This is only half the area we need though, as we get the shape above from cutting the rectangle along the diagonal, so the final answer will be
8
.
Sahi khel Gaya ......
I tried just like it and BINGO.
Got it correct...
Anyway check out my profile.... I have 2 sums waiting...
Really the incarnate of Issac Newton
Let's consider the rectangle in the x y plane with ( 0 , 0 ) , ( 3 , 0 ) , ( 3 , 4 ) , ( 0 , 4 ) as vertices. We can find the parabola parametric equation using the Bèizer curve equation
c ( t ) = j = 0 ∑ 2 ( j 2 ) t j ( 1 − t ) 2 − j p j
where p 0 = ( 3 , 0 ) , p 1 = ( 0 , 0 ) , p 2 = ( 0 , 4 ) . Solving the equation we have
c ( t ) = ( 3 t 2 − 6 t + 3 , 4 t 2 ) , t ∈ R , t ∈ [ 0 , 1 ] .
Now, the area of the interested region can be considered as the difference between the area of the rectangle and the area of the two triangoloid in the picture. So we can write
A r e a = 1 2 − 2 ∫ 1 0 4 t 2 ( 6 t − 6 ) d t = 8 .
The integral has been derived substituting f ( x ) = 4 t 2 and x = 3 t 2 − 6 t + 3 into ∫ a b f ( x ) d x . I inverted the integral index because the curve is traveled from ( 3 , 0 ) to ( 0 , 4 ) , otherwise, using ∫ 0 1 the triangoloid area would have been negative.
As you defined p 0, p 1, p 2 parametric function is c(t)=(3t^2,4t^2-8t+4), which is the same curva but defined inversly. I mean you had to say p 0=(3,0), p 1=(0,0), p 2=(0,4).
Log in to reply
Yes, you're right! I switched p0 and p2, thank you for reporting it!
I've got a cheating solution, making use of the format of the answer required being an integer.
Look below and you will get it immediately. Basically you can see the integer that best fit this approximation is 8. Even if it was 7 or 9 you got 3 tries ;)
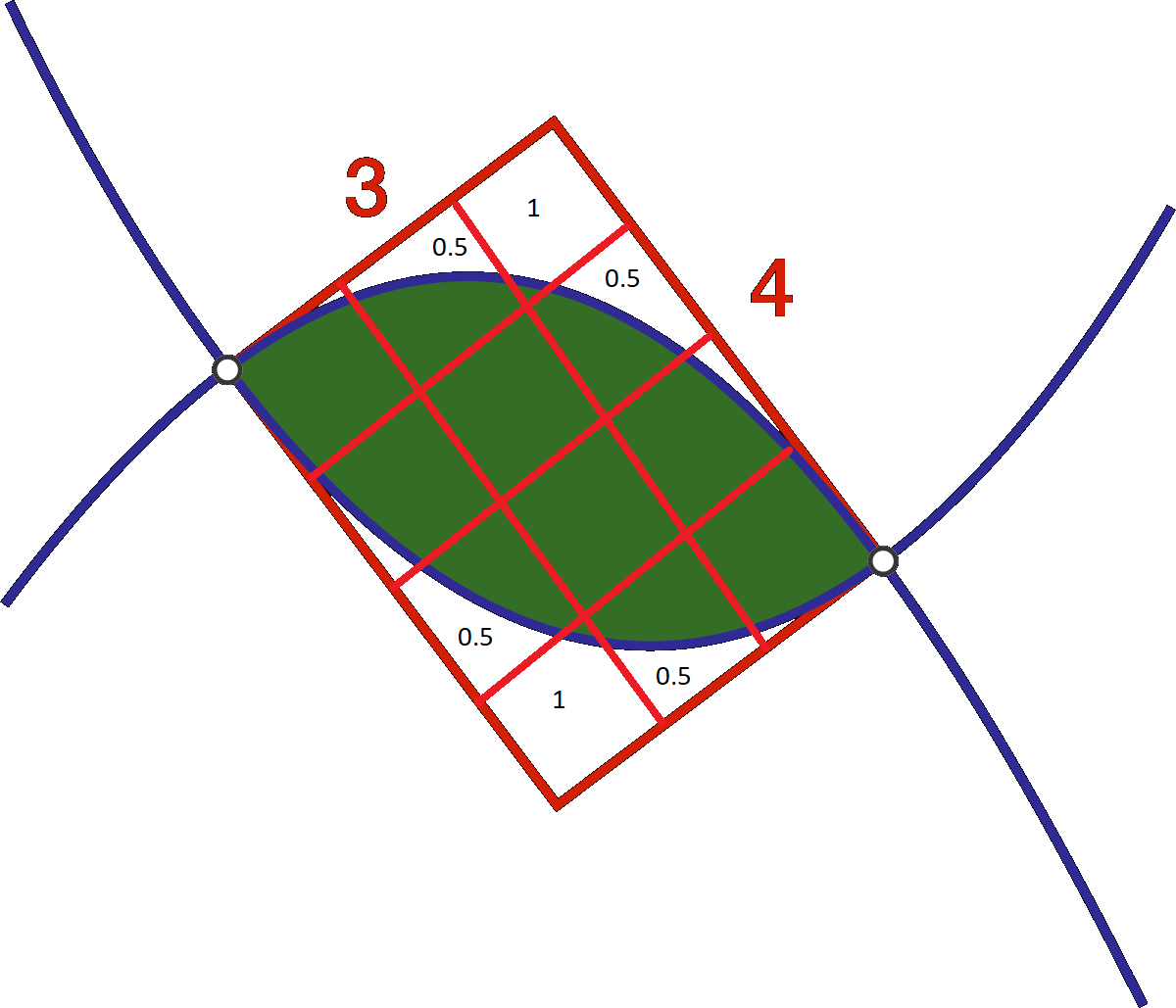 .
.
Take two points on a parabola, and draw the tangents to the parabola at these points. Then the area of the parabolic segment is equal to 2/3 the area of the triangle formed by the two points and the intersection of the tangents.
Hence, the area is simply 2 / 3 ⋅ 1 2 = 8 .