Boxes

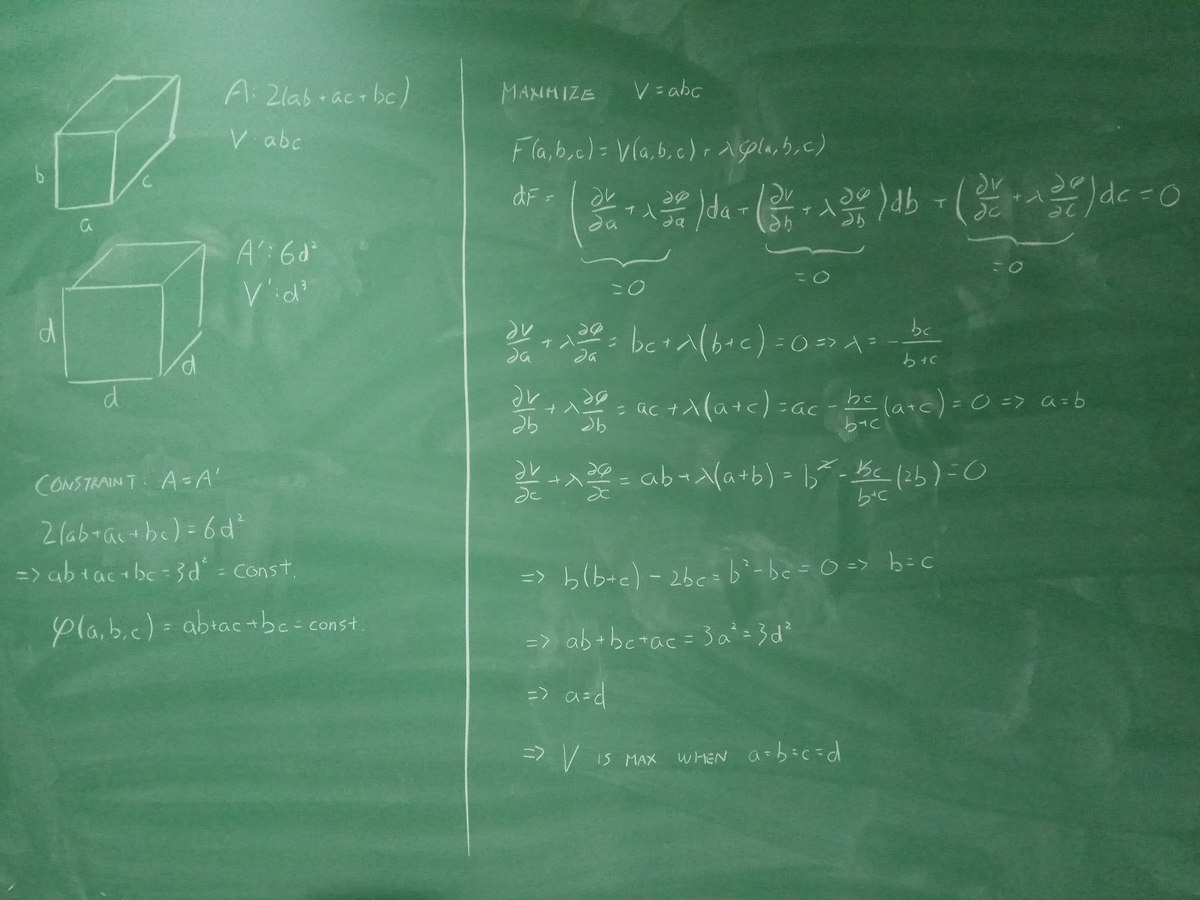
Let side of length of cube is $a$ and dimensions of cuboid is $p,q,r$ where these three not all equal.

So, $6 a^2=2(pq+rq+pr) > 2.3 (pqr)^{2/3}$ (Using AM-GM) equality will not be there because these three can not be equal then this will become a cube.

$a^2 > (pqr)^{2/3} => a > (pqr)^{1/3} => a^3 > pqr \implies$ Volume of Cube > Volume of Cuboid

let $2,3$ and $5$ be the dimensions of the cuboid. so the surface area is $2[2(3)+3(5)+2(5)]=62$ and the volume is $2(3)(5)=30$ .

from the surface area of the cuboid, the side length of the cube is $\sqrt{\dfrac{62}{6}}=\sqrt{\dfrac{31}{3}}$ so the volume of the cube is $\approx 33.22$

$\huge\therefore$ $\text{With equal surface areas, the cube has a larger volume.}$

You can use a Lagrange multiplier.