Boxxed by the Kube!
A cuboid contains a sphere of radius 2 and four unit spheres. The spheres are tangent to each other and to the box.
The height of the box can be expressed as , where A and B are coprime positive integers. Find .
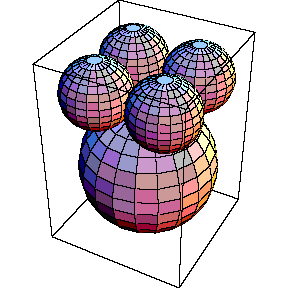
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider a right triangle with the right angled corner at the center between the four unit spheres, the shorter side terminating at the center of one of the unit spheres, and the longer side terminating at the center of the sphere of radius 2. Let h be the height of the box. Then
a = 2
b = h − 1 − 2
c = 1 + 2
and we solve for h in this Pythagorean equation
a 2 + b 2 = c 2
which fairly quickly gets us h = 3 + 7 , and so the answer is 1 0
This is the quadruple Mickey Mouse, isn't it?