Boy meets girl
Two brothers, Adam and Alex, each ride a motorbike which can travel 300 km on a full tank of fuel. They got to know a sweet pretty girl called Brenda and invited her over to their place. She said yes, and so the brothers set off from their house on their motorbikes with full tanks for Brenda's house.
They had a pact: they could transfer fuel between their bikes but cannot detour to refill their tanks. Also, only one of them is needed to fetch Brenda from her house but both motorbikes must be back at the two brothers' house.
What is the maximum distance between the brother's house and Brenda's house such that they can pick her up and bring her home?
Assume that the efficiency of the motorbikes' fuel tanks remains the same, even with Brenda riding pillion.
The answer is 200.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
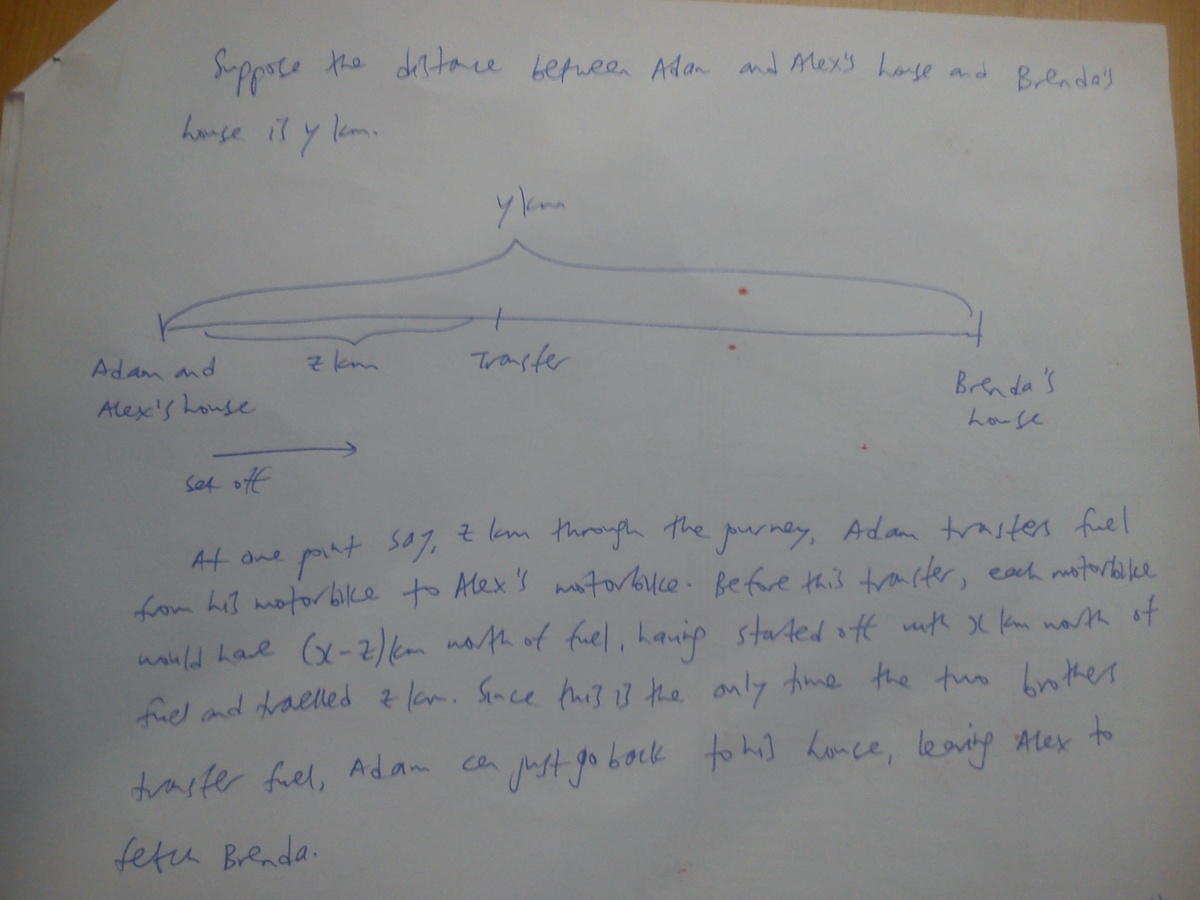


We think like this, if only one bike is needed to actually pick Bee up, then the other bike would just serve as reserve fuel tank (or R in short) for the "real" carrier (let this be C). So R's max distance x would have to cover both R's own 2-way journey (between home base, H and some point in between to Bee's house) and a portion of C's returning one. To maximize the reachable distance they need to optimize the fuel utilization, and that means not only both depleted their resources at the end of the journey, but the "rendezvous" point P also has to be the exact place when C's oil run out. Meaning that R's fuel covered for one HP journey and 2 PH journey, a total of 3 same distance totaling at x. Thus, HP = x/3. Now let's go back to C and its fuel consumption. The boys rode together up to point P from H, so x/3 of C's would have been emptied by that time (and place). The remaining 1-x/3 = 2x/3 would have to be enough to cover the return / 2-way journey from P to Bee's back to P (easier to see P->B->P). 2x/3 divide by 2 for 1 maximum distance PB equals x/3.
HP = x/3
PB = x/3
Total distance = HP + PB = x/3+x/3 = 2x/3
Answer = 2+3 = 5