Braided Geometrical Sequences of Circles
Inside a wedge, both blue and red infinite sequences of circles have radii that increase in geometrical progression by a factor of 2 .
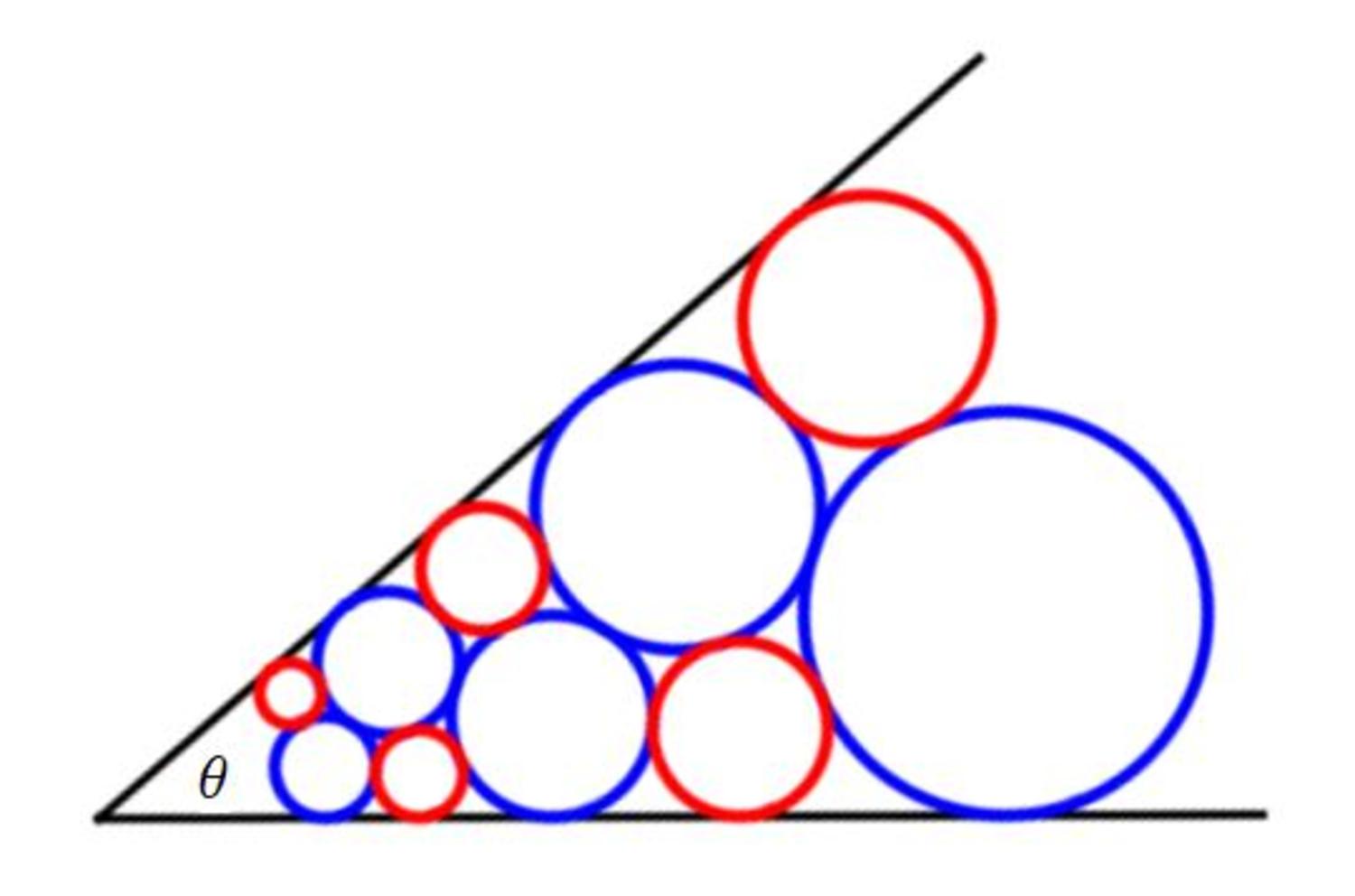
In degrees, what is the angle θ of the wedge?
This figure is self-similar, i.e., e.g., it's similar to itself when doubled in size. The circles are tangent to each other and to the wedge as shown.
The answer is 40.61079749357.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is definitely shorter than my solution. But, curiously, yours involves a cubic, and mine does not. I'm going to have another look at this, comparing the two end results.
Log in to reply
Oops. It is quadratic, not cubic. My solution has been amended/expanded. Since we get a nice formula for t = tan 2 1 θ in terms of p , we can do the necessary simplification quite easily...
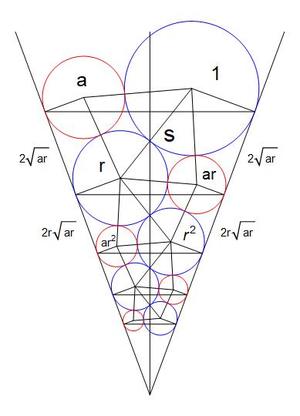
Let
a
,
1
,
a
r
,
r
,
a
r
2
,
r
2
.
.
.
be the radii of the circles, where
r
is the geometric ratio, here equal to
2
1
.
Let
s
be the slope of the line between centers of circles
1
,
r
.
The distances between the points where circles
a
,
r
and
1
,
a
r
are tangent to the wedge are
2
a
r
.
The distances between the points where circles
r
,
a
r
2
and
a
r
,
a
r
3
are tangent to the wedge are
2
r
a
r
.
Etc. Hence, the triangles formed by the apex of the wedge and where pairs of circles are tangent to it are isosceles.
By symmetry, the tangents of circles
1
,
r
,
r
2
,
.
.
.
are colinear.
Given an arbitrary slope
s
, the coordinates of centers of circles
1
,
r
,
r
2
,
.
.
.
can be found.
From this, we can find the distance between the tangents of circles
1
,
r
,
r
2
.
.
to the wedge can be found.
From this, the radius
a
can be determined, and the coordinates of the circle
a
r
can be found.
From this, the distance between centers of circles
r
,
a
r
can be found, and compared with length
r
+
a
r
.
By such means, an exact answer for
s
is possible.
Once we have
s
, we can find the apex angle of the wedge.
The calculation is very rigours.
Yeah. Maybe I'll post the full exact answer later.
Suppose that distance of the points of tangency of the two circles of radius r and R from the vertex are x and X respectively. Considering the two right-angled trapezia (marked in orange) we deduce that X 2 − x = x 2 − X = 2 2 r R = 2 4 5 r R so that x = X = 2 − 1 2 4 5 r R ( 1 ) Considering the two pairs of congruent right-angled triangles (marked with dotted lines) we deduce that θ = 2 tan − 1 ( X r ) + 2 tan − 1 ( X R ) ( 2 ) The fact that the line P Q has length R ( 1 + 2 ) means, by choosing a suitable coordinate system, that X 2 ( 3 − 2 2 cos θ ) − 4 2 X R sin θ = 2 2 R 2 ( 1 − cos θ ) ( 3 ) Equation (1) tells us that the circles are all tangent to the two straight lines. Equation (2) tells us that a pair of red and green circles bridges the gap between the two lines, while equation (3) ensures that successive green circles are tangent with each other.
Eliminating variables from equations (1), (2) and (3) gives us a quadratic equation for p = ( X R ) 2 , namely 1 2 8 2 p 2 − 3 2 ( 3 − 2 2 ) p − ( 3 − 2 2 ) = o which has one positive and one negative real root, and hence there is a unique positive value for X R . Moreover X r and θ are determined uniquely by X R . Solving we obtain X R = 4 1 3 2 − 4 + 3 0 − 2 1 2 and so X r = 0 . 1 3 6 3 4 6 X R = 0 . 2 2 2 4 5 θ = 4 0 . 6 1 0 8 ∘