brain teaser 4
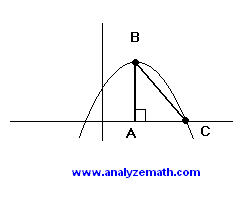The right triangle ABC shown below is inscribed inside a parabola. Point B is also the maximum point of the parabola (vertex) and point C is the x intercept of the parabola. If the equation of the parabola is given by y = -x2 + 4x + C, find C so that the area of the triangle ABC is equal to 32 square units.
problem 3.
The answer is 7.544.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
h = -b / 2a = 2 : x coordinate of the vertex of the parabola k = -(2)2 + 4(2) + C = 4 + C : y coordinate of vertex x = (2 + sqrt(4 + C)) , x = (2 - sqrt(4 + C)) : the two x intercepts of the parabola. length of BA = k = 4 + C length of AC = 2 + sqrt(4 + C) - 2 = sqrt(4 + C) area = (1/2)BA * AC = (1/2) (4 + C) * sqrt(4 + C) (1/2) (4 + C) * sqrt(4 + C) = 32 : area is equal to 32 C = 12 : solve above for C.