Break my code
Computer Science
Level
3
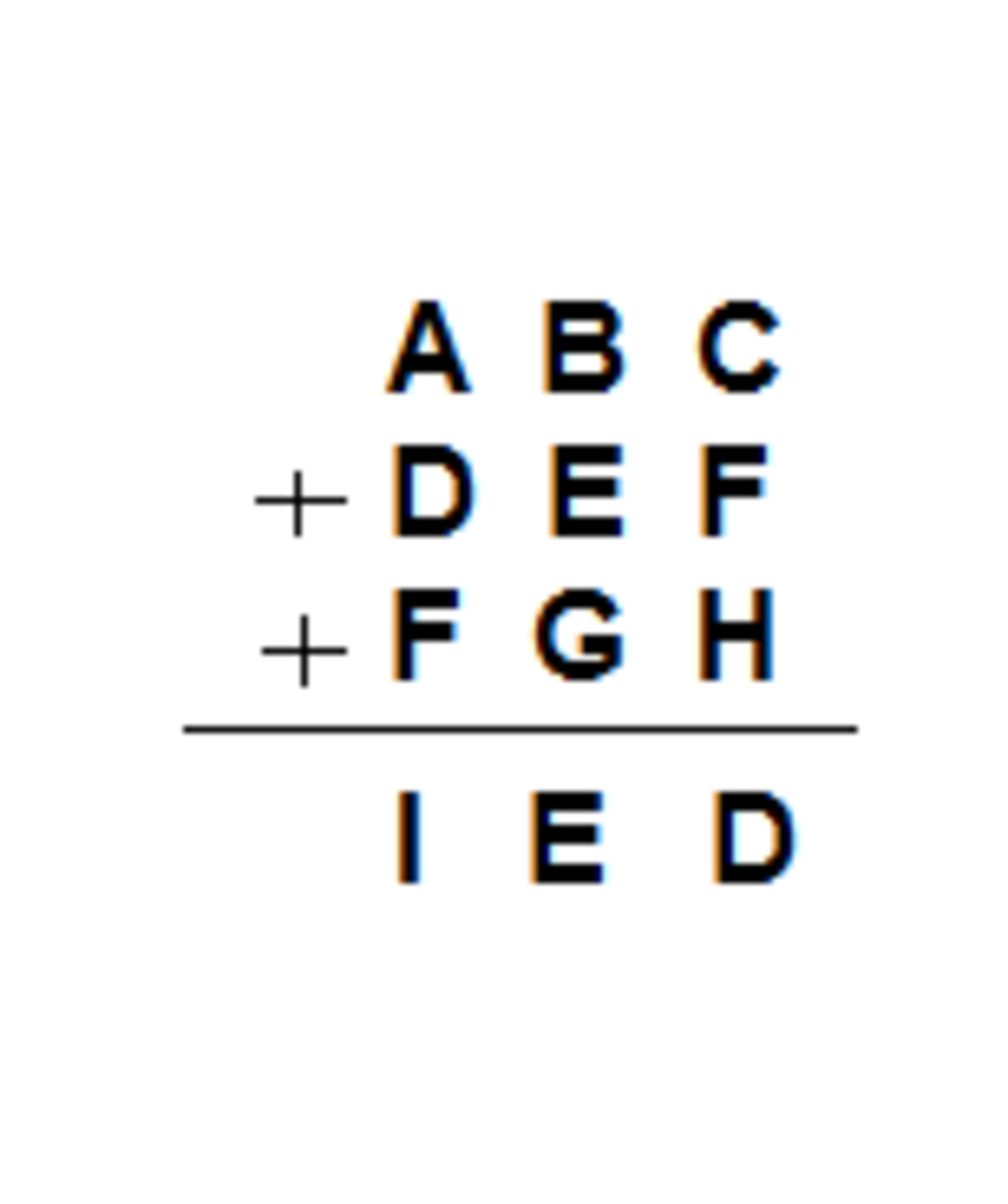
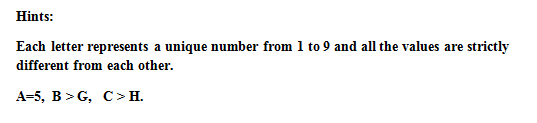
Tthe answer must be given in the numerical form of ABCDEFGHI.
The answer is 567281349.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Actually this is a mathematical problem that I found on the internet this is the actual link where I took it from http://www.scienceforums.net/topic/37997-math-cryptogram/
Given that A = 5, D ≠ 0, F ≠ 0, D ≠ F, I=5+D+F the smaller value that can reach I is 8 and the biggest is 9, we conclude that: I ∈ [8, 9], actually as the last digit of the sum of B, G and E equals to E we now can conclude that I equals to 9 as the sum of B,G equals to 10 or the sum of B,G,1 equals to 10. Therefore we know that I=9, and that D, F ∈ [1, 2]. Now in the second column we have that the last digit of the sum of B, G, and E is E and so B+G must be equal to 10 o 9 this is because B ≠ 0, G ≠ 0 and B + G ≤ 17 and it can be 9 since the C, F, H can be bigger or equal to 10, since B > G we conclude that B ∈ [7, 6], G ∈ [3, 4]. Finally we reach the last column and we that C + F +H = X D and since we know that D is equal 1 or 2 we quickly realize that X = 1 and that the sum equals either to eleven or to twelve we notice that now the sum of B+G must be equal to 9, since the only way of combining those two values of B and G is B=6 and G=3 and since C > H we conclude that C=7 and H=4 and therefore 7+4+F= G with our first conditions means that F=1 and D= 2 quickly because 11+1=12 but 11+2 ≠ 11 finally the last digit we have left is 8 so 8= E and that´s how it is done. A = 5, B = 6, C= 7, D = 2, E = 8, F = 1, G = 3, H = 4 , I=9. Therefore the solution of the equivalence numerical form of ABCDEFGHI is 567281349