Breaking the chain
Consider an infinite chain of alternating charges (
+
q
,
−
q
,
+
q
,
−
q
…
) and spacing
d
. It is known that the interaction energy between two neighboring charges is
E
p
=
−
1
J
. What is the work needed
in Joules
to remove one of the charges from the chain and place it at infinity?
Hint:
ln
(
1
+
x
)
=
−
∑
k
=
1
∞
(
−
1
)
k
k
x
k
.
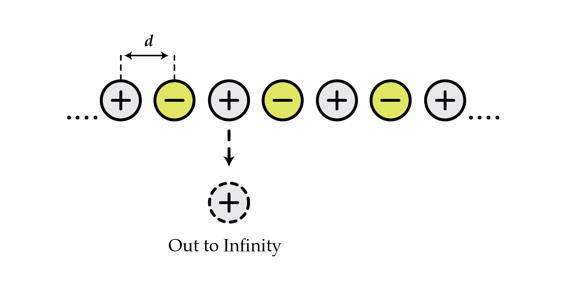
The answer is 1.386.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Discussions for this problem are now closed
The work necessary to remove the charge and place it at infinity is the difference between the potential energy in infinty and in the chain, in other words: U ∞ − U c h a i n = W .
The potential energy is given by U = d k . q 1 . q w . When d goes to ∞ the potential energy goes to 0, so: 0 − U c h a i n = W .
Now we only have to figure out the potential energy in the chain. Knowing that the potential energy between two neighbouring charges is − 1 J and the distance between the charges is always d, we can write it as: 2 . ∑ ( − 1 + 2 1 − 3 1 + 4 1 − 5 1 . . . )
Note that the alternating signals in the sum come from the alternating signals in the charges, the denominator increasing by 1 comes from the increasing distance and the 2 multiplying the sum happens because there are charges in both sides.
We can rewrite the sum as 2 . k = 1 ∑ ∞ ( − 1 ) k k 1 k = − 2 . l n ( 1 + 1 ) = U c .
As shown in the beggining U c = − W ⟺ W = 2 . l n 2 = 1 . 3 8 6 J
A chain of alternating charges allows us to use symmetry and superposition to simplify the problem. To find the work needed to free a single charge is defined as the applied force times the displacement, for electric charges we can write this as:
W = ∫ r 0 ∞ ( − 4 π ε 0 1 r 2 q q ′ ) d r = 4 π ε 0 1 r 0 q q ′
This is just the potential energy between the two charges which was give earlier, so we can write:
E p = 4 π ε 0 1 r 0 q q ′ = − 1 J
To calculate the total work we need to add all the potentials from each charge in the chain. The total work can be broken up into to parts, contributions from the right side and left side:
∑ W = ∑ W R i g h t + ∑ W L e f t
Due to the symmetry of the chain the left and right sides will be identical, therefore we can calculate just the right side of the chain and then double it to obtain the total work:
∑ W = 2 ∑ W R i g h t = 2 ∑ ( E p ) R i g h t
The total work for the right side of the chain is given by:
∑ W r i g h t = 4 π ε 0 1 d q q ′ [ 1 − 2 1 + 3 1 − 4 1 + ⋯ + n 1 ] = − E p [ 1 − 2 1 + 3 1 − 4 1 + ⋯ + n 1 ]
Using the identity given above:
ln ( 1 + x ) = − ∑ k = 1 ∞ ( − 1 ) k k x k
In our case x=1, this gives us:
∑ W r i g h t = − E p [ 1 − 2 1 + 3 1 − 4 1 + ⋯ + n 1 ] = ln ( 2 )
The total work is double this, therefore:
∑ W = 2 ln ( 2 ) = 1 . 3 8 6 ( J )
We calculate the total internaction energy related to the charge we remove. We do this by calculating the interaction energy between each charge and the to-be-removed charge. (Interaction energy = Potential Energy)
Because of symmetry, we will find the total energy with the right side and double that to get the total interaction energy.
The interaction energy between two neighbouring charges is given by E p = d k ( q ) ( − q ) = − 1 J .
For a charge 2 d down, the charges have the same sign and have E = 2 d k ( q ) ( q )
For 3 d , you have E = 3 d k ( q ) ( − q )
This will go on forever. The sign will alternate each time and the denominator will increase by one d . Now you add it all up and remember to multiply by two.
E t o t a l = 2 ( d k ( q ) ( − q ) + 2 d k ( q ) ( q ) + 3 d k ( q ) ( − q ) − 4 d k ( q ) ( q ) . . . )
E t o t a l = 2 ( d k ( q ) ( − q ) ) ( 1 − 2 1 + 3 1 − 4 1 . . . )
E t o t a l = 2 E p ( 1 − 2 1 + 3 1 − 4 1 . . . )
Now we can use the hint to turn the infinite sum on the right side into a nice evaluable function. Using the hint we plug in x = 1 to the summation and find the sum is equal to ln(2) .
E t o t a l = 2 ( − 1 J ) ln(2) = − 1 . 3 8 6 J
To remove the charge to inifinty, we have to do work to bring it up to zero potential.
W = Δ E = 0 − E t o t a l = 1 . 3 8 6 J
(Note: the hint comes from the Maclaurin expansion of the ln( x + 1 ) )
Work Done + Change in potential energy = Change in kinetic energy
Here change in kinetic energy can be assumed to be zero. So our equation reduces to
* Work = -Change in P.E *
* Given : d − k q 2 = -1J *
Lets calculate the initial potential energy of the charge.
For that, we will superpose the potential due to positive charge altogether with the potential due to the negative ones.
So, potential energy due to the other positive charges on the charge spoken about =
2 × ( 2 d k q 2 + 4 d k q 2 + 6 d k q 2 .......... till infinity
(* Multiplication by two implies, addition of energies due to charges on left and charges on right*)
And PE of the charge due to the negative charges =>
2 × ( d − k q 2 + 3 d − k q 2 + 5 d − k q 2 ... till infinity
Using the superposition principle, we can say the net P.E = P.E due to positive charges + P.E due to the negative ones.
Therefore, summing them up, we get =2( d − k q 2 + 2 d k q 2 + 3 d − k q 2 + 4 d k q 2 + 5 d − k q 2 + 6 d k q 2 ) .... till infinity.
Taking d 2 k q 2 out of the bracket, we get :
d 2 k q 2 ( d − 1 + 2 d 1 + 3 d − 1 + 4 d 1 + 5 d − 1 + 6 d 1 ) .... till infinity.
*This series resemble -ln(1+x) for x = 1 * .
Therefore, the series reduces to * d 2 k q 2 (-ln(2)) * = 2 × − 0 . 6 9 3 =1.386
(*Value of ln2 = 0.693)
Potential energy at infinity is almost equal to zero. So, the change in Potential energy will be :
Final P.E (i.e, "0") - Initial P.E ( i.e, 1.386) = -1.386.
So, recalling our early equation,
* Work = -Change in P.E * = * -(-1.386) *
=1.386
And, we're done.. Finally!!
In order to find the total work needed to remove the charge, we need to find the amount of potential energy the charge has with respect to infinity (and thus how much energy we need to put in to move the charge to infinity). To do this, we need to sum the charge's potential energy with respect to every charge in the chain.
We know that the potential energy between any two arbitrary point charges is r k q Q . I'm going to look at the right half of the chain first. We know that each charge in the chain has the same q , every n th charge is located a distance n d away from the charge we care about, and the charge signs alternate starting with negative. Thus, the potential energy of that charge with respect to the right half of the chain should be − d k q 2 + 2 d k q 2 − 3 d k q 2 . . . or ∑ n = 1 ∞ ( − 1 ) n n d k q 2 . Since the left half of the chain is the same as the right half, the energy of the charge we care about with respect to the entire chain is just twice of half the chain, or 2 ∑ n = 1 ∞ ( − 1 ) n n d k q 2 .
But wait! We know the interaction energy between any two neighboring charges is − 1 J . Interaction energy is the potential energy with the respect to just those charges (so really, our summation up there is a sum of interaction energies), and so we know that d k q 2 = − 1 .
We can substitute that into our original expression for the chain's potential energy to find 2 n = 1 ∑ ∞ ( − 1 ) n n d k q 2 = 2 n = 1 ∑ ∞ ( − 1 ) n n − 1 = − 2 n = 1 ∑ ∞ ( − 1 ) n n 1 n = 2 ( − n = 1 ∑ ∞ ( − 1 ) n n 1 n ) . This matches the form of the infinite series in the hint we were given when x = 1 , and so simplifies into 2 ln ( 1 + 1 ) or ln ( 4 ) .