Bridges of Konigsberg

Probability Level 1

Is there a walking path that stays inside the picture and crosses each of the bridges exactly once?

No Yes

View wiki
Eli Ross by Eli Ross

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Eli Ross Staff
Aug 23, 2016

After trying and failing to draw such a path, it might seem plausible that the task is impossible. But how can this be proven, and what happens if the configuration is modified in some way?

For a solution and discussion, check out the wiki on Eulerian paths !

11 Helpful 0 Interesting 1 Brilliant 1 Confused

This is the famous Köningsbergerproblem.

Peter van der Linden - 4 years, 9 months ago

Isn't this more of a topology problem ? I think this is one of the problems which pointed to the way of understanding and motivated the invention of topology anyway.

A A - 4 years, 9 months ago

Log in to reply

It's both! Basically, the problem can be reduced to this graph, which gave way (relatively immediately) to a bunch of ideas in Graph Theory :

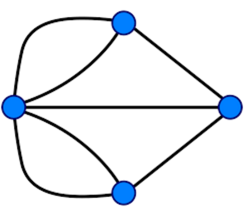
But, like you're alluding to, Euler's idea that the relevant information was the number of bridges and the list of their endpoints (rather than their exact positions) was the type of reduction/transformation that eventually inspired some of the basic ideas in Topology .

Eli Ross Staff - 4 years, 9 months ago

Log in to reply

Haha ,yes I suppose I have to agree with you that it's both anyway.

I like characterizing the "reduction/transformation" you talk about as having it's origin in conceiving or almost touching if not explicitly getting it the idea that the object of which it is talked is that of structure by/in it's a priori form or of structure as it is perceived in the immediacy of the act of thinking it by virtue of it's form, and as such that topology as domain had it's origin not so much in making a simple reduction or exteriorly done transformation lacking substantial content but in a subtle observation which assured the conceiving of a new and by the depth of insight into the working and intimacy of what "structure" is even more abstract conception that has it's own innate irreducible dignity anyway .

A A - 4 years, 9 months ago
Tommy Finney
Jun 28, 2018

It has more than two odd nodes, so an Eulerian path is not possible..

5 Helpful 0 Interesting 1 Brilliant 0 Confused
Khalid Hassani
May 21, 2020

A graph has an Euler path if and only if there are at most two vertices with odd degree. It's not the case here.

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Lâm Lê
Sep 19, 2020

Because the light-green islands have 3 3 edges and the dark-green island has 5 5 , an Eulerian path is not possible.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Okay, let’s establish a rule that should be obvious. For any bridge you use to enter in, you need one to leave. That means bridges come in pairs. The only exception is beginning and the part you end at, it could have an odd number of bridges connected, so at most 2 landmasses. Looking at this diagram, every land mass has an odd number of bridge, thus it is impossible.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Professor Ss
Oct 25, 2016

There is no exact solution of this problem.....but u can established a graph model of this problem.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...