Bright lights

Geometry Level 4

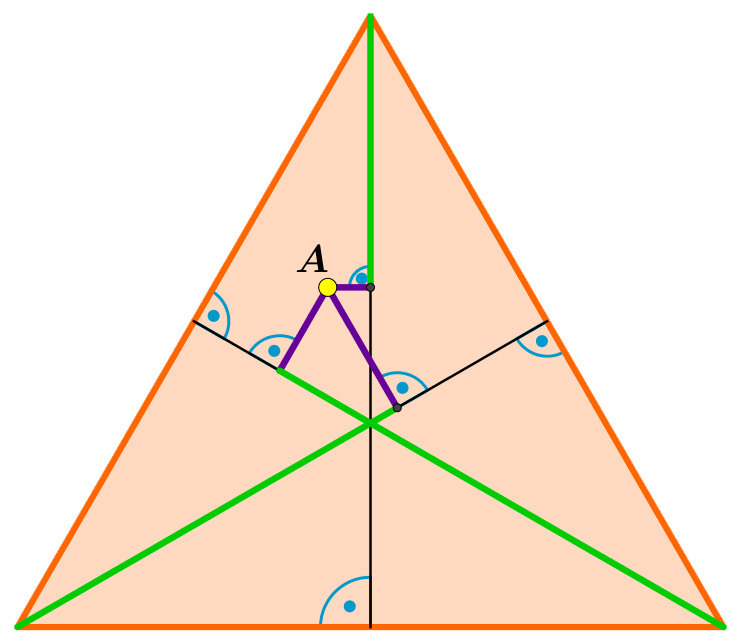
$A$ is a random point inside the orange, equilateral triangle. Drop perpendicular to each of the medians. The green segments connect each vertex to the foot of the perpendicular along the corresponding median.

What is the sum of the lengths of the green segments equal to?

This is part of the series " It's easy, believe me! "

The sum of the lengths of the purple segments

\frac{2}{3}

the length of the perimeter of the orange triangle Half the length of the altitude of the orange triangle Half the length of the perimeter of the orange triangle Twice the length of the altitude of the orange triangle It depends on the coordinates of point

A

1 solution

Maria Kozlowska
Oct 15, 2017

Point $A$ , feet of perpendiculars and centroid are concyclic. Feet of perpendiculars form an equilateral triangle. Sum of green segments within this circle is equal to the other segment between the centroid and a foot of a perpendicular (their angles are 60 and 60). This means that the full green segments are equal to 3 times circumradius of the large triangle.

Bright lights

1 solution

0 pending reports