Brightest bulb
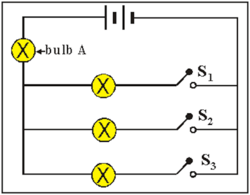 Jane connected four identical light bulbs in a circuit as shown above. She observes that the brightness of bulb
varies if some of the switches are closed. In which case will bulb
burn brightest?
Jane connected four identical light bulbs in a circuit as shown above. She observes that the brightness of bulb
varies if some of the switches are closed. In which case will bulb
burn brightest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The brightness of bulb A is proportional to P the power consumed by it or I 2 the square of the current flowing through it. Let the supply voltage be V and the resistance of the bulb be R , then the current I is given by:
I = R + n R V
where n = 0 , 1 , 2 , 3 is the number of switches S 1 , S 2 , S 3 are closed.
I is maximum when ( R + n R ) is the lowest, that is when n = 3 .
Therefore, bulb A is the brightest when a l l S 1 , S 2 , S 3 a r e a l l c l o s e d .