Brilliant and Problem Solvers
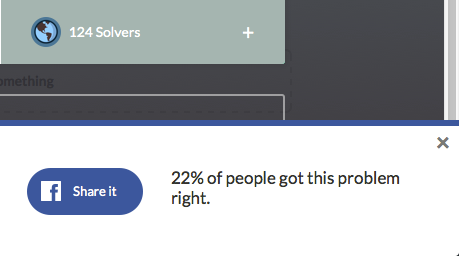 The above picture shows (as of 12/15/14) the number of solvers of the first problem I posted on Brilliant,
Yay for 2014! #1
. The percentage in the box below the number of solvers is the percentage of viewers who solved the problem.
The above picture shows (as of 12/15/14) the number of solvers of the first problem I posted on Brilliant,
Yay for 2014! #1
. The percentage in the box below the number of solvers is the percentage of viewers who solved the problem.
Now, this percentage isn't an exact figure; in fact, if the exact percentage of viewers that solved the problem is then the percentage that appears in the box is For example, if the number of viewers on a particular problem is 7, and 3 of those viewers solve it, the percentage in the box would be when in fact the exact percentage is
Given this, the sum of all the possible number of viewers that could possibly have viewed my problem is equal to Find the last two digits of
Notation : denotes the floor function .
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The percentage of viewers who solved the problem, written as a decimal, can be written as V S , where S is the number of solvers and V is the number of viewers. In this case, our fraction is V 1 2 4 . Thus, all integers V such that 1 0 0 2 2 ≤ V 1 2 4 < 1 0 0 2 3 will satisfy our problem. Solving this yields
5 3 9 2 3 3 ≤ V < 5 6 3 1 1 7 .
Since V is an integer, 5 4 0 ≤ V ≤ 5 6 3 , and our sum is 5 4 0 + 5 4 1 + ⋯ + 5 6 3 = 1 3 2 3 6 .
(The actual number of viewers on the problem, as of 12/15/14, is 557.)