Brilliant Games - Quarter Quell 2
What is the value of
1 − 4 1 + 4 2 1 − 4 3 1 + 4 4 1 − … ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
That's a nice approach of dealing with GP's with a negative term (other than substituting in the formula directly, of course).
x = 1 − 4 1 1 + 4 2 1 − 4 3 1 + 4 4 1 − … 4 x = 4 1 1 − 4 2 1 + 4 3 1 − 4 4 1 + 4 5 1 − … x + 4 x = 1 + 4 1 1 − 4 1 1 + 4 2 1 − 4 2 1 … x + 4 x = 1 4 x + x = 4 5 x = 4 x = 5 4
Nice solution :)
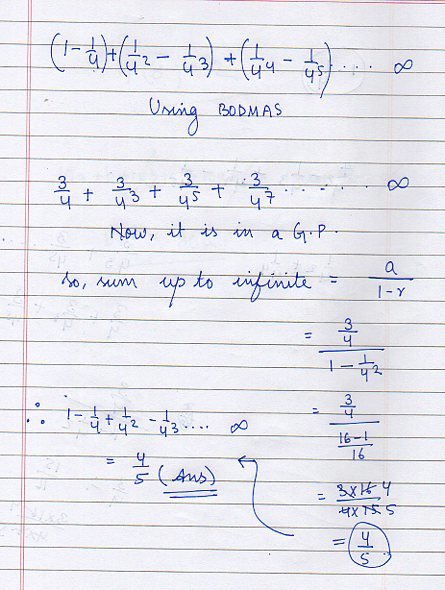
What about this !!!!!!!!!!!!!!!!
Coolest solution ever!
Solution to geometric series
a/(1-r)
a = 1
r = 1/4
I used this too! Just finished calc 2 so this was the first thing to come to mind!
Let 1 − 4 1 + 4 2 1 − 4 3 1 + 4 4 1 − . . . . . . . = x
Multiplying both sides with 1 6 , we get
1 6 − 4 + 1 − 4 1 + 4 2 1 − 4 3 1 . . . . . . . = 1 6 x ⇒ 1 6 − 4 + ( 1 − 4 1 + 4 2 1 − 4 3 1 . . . . . . . ) = 1 6 x ⇒ 1 6 − 4 + x = 1 6 x ⇒ 1 2 + x = 1 6 x ⇒ 1 2 = 1 5 x ⇒ 1 5 1 2 = x ⇒ 5 4 = x