Triangle

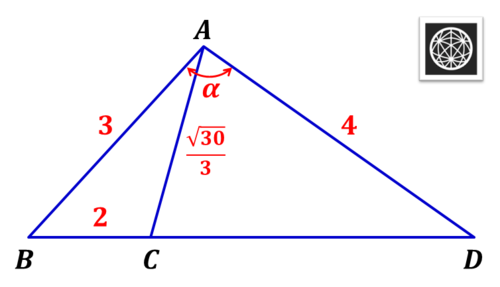See the picture above. First, we calculate $m$ by using Stewart's theorem : $$ $b^2m+c^2n=a(d^2+mn).$ $$ We obtain $m=4\text{ cm}$ , then using cosine formula yields $$ $\cos\alpha=\frac{b^2+c^2-a^2}{2bc}=-\frac{11}{24}.$ $$ Therefore, using trigonometric identity $$ $\sin^2\alpha+\cos^2\alpha=1,$ $$ we obtain $$ $\sin\alpha=\sqrt{1-\cos^2\alpha}=\frac{\sqrt{455}}{24}.$ $$ Thus, $p-q=455-24=\boxed{\color{#3D99F6}{431}}$ . $$

$\text{\# }\mathbb{Q.E.D.}\text{ \#}$

$Applying \ Sin\ and\ Cos\ Rules\ and\ Sin^2A+Cos^2A=1\ the\ following\ angles\ are\ found.\\ In\ \Delta ABC,\\ CosB=\dfrac{2^2+3^2-\frac{10} 3}{2*2*3}=\dfrac{29}{36}.\ \ \ \implies\ SinB=\frac 1 {36}*\sqrt{36^2-29^2}=\dfrac{\sqrt{455}}{36}\\$ $In\ \Delta ABD,\ \ \\ SinD=SinB*\dfrac{AB}{AD}=\dfrac{\sqrt{455}}{36}*\dfrac 3 4=\dfrac{\sqrt{455}}{48} \ \ \ \implies\ CosD=\frac 1 {48}*\sqrt{48^2-455}=\dfrac{43}{48}\\ \therefore\ Sin\alpha=Sin(B+D)=SinB*CosD+CosB*SinD\\ =\dfrac{\sqrt{455}}{36}*\dfrac{43}{48}+ \dfrac{29}{36}* \dfrac{\sqrt{455}}{48}\\ =\dfrac{\sqrt{455} *(43+29)}{36*48}=\dfrac{\sqrt{455} *72}{36*48}=\dfrac{\sqrt{455}}{24}=\dfrac{\sqrt{p}}{q} \\ p-q=455-24=431.$

I manually solved the angles

Use cosine rule for triangle ABC and find angle B then use again cosine rule for triangle ABD to find the length BD. Once more use cosine rule to find angle 'alpha'.