Brilliantian Graphing System
It was recently discovered that the citizens of the lost city of Brilliantia developed a unique graphing system in which the -, -, and -axes were placed at intervals on a two-dimensional plane. To graph an point, the Brilliantians would start at the origin and measure units in the in the positive direction, then from that point measure out units in the positive direction, and then from that point measure out units in the positive direction. The point in the Brilliantian system is shown below:
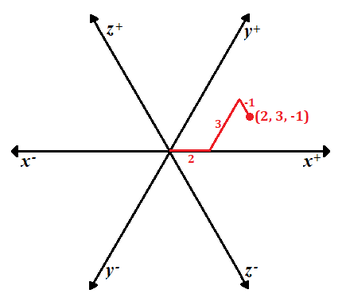
If the area of the region defined by in the Brilliantian system for positive real values of , , and can be expressed as , where is an integer and is a square-free integer, find .
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Proof by optical illusion (thanks to GeoGebra):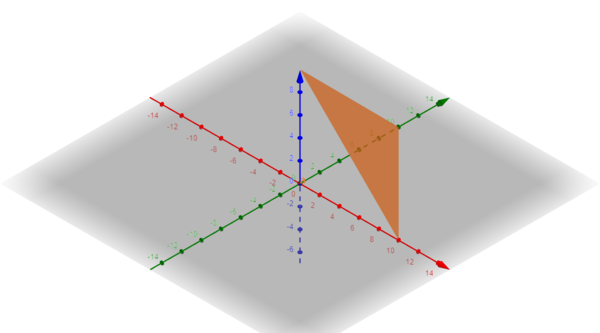
Is this a plot of x + y + z = 1 0 on Brilliantia? Or one in 3D? Either way, we can see that the orange region is an isosceles triangle with two sides of length 1 0 separated by an angle 1 2 0 ∘ , so its area is 2 5 3 giving the answer 2 8 .