Brilliantia's Buildings
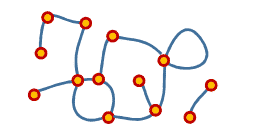
On the island of Brilliantia , the basic building element is a woven wall of fronds supported at each end by a vertical pole. A single pole may support a number of walls radiating from it. A room is any continuous area completely surrounded by walls. A collection of connected walls makes up a building.
How many buildings are on the island if 345 walls, supported by 234 poles, surround 123 rooms?
Details and Assumptions:
-
Every wall must be supported on both ends, but this can be done by a single pole.
-
Walls may not cross each other.
-
A building which is completely surrounded by another building but is not attached to it counts as a separate building.
-
A building does not need to contain any rooms. A standalone wall, for example, counts as a building.
-
Outdoors does not count as a room.
-
A pole may not stand alone.
For example in the above diagram there are 14 walls, 13 poles, 3 rooms, and 2 buildings.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Outline of the calculation:
For every building the number of poles, P , the number of rooms, R , and the number of walls, W , satisfy the equation:
P + R − W = 1
So since overall P + R − W = 2 3 4 + 1 2 3 − 3 4 5 = 1 2 , this can only happen if there are 1 2 buildings.
Derivation of the equation:
Any building can start only by first putting up a single wall. There are two kinds of walls. A wall supported by two poles will have P = 2 , R = 0 , W = 1 . A wall supported by just one pole will have P = 1 , R = 1 , W = 1 . So in either case there is just one wall for two items of the other kind, and P + R − W = 1 .
When expanding a building with a new wall-
(1) we can attach the new wall on both ends to a single existing pole. This generates one new room, no new poles, and one new wall. So the value of P + R − W remains unchanged.
(2) we can attach the two ends of the new wall to two existing poles. This generates one new room, no new poles, and again one new wall. P + R − W again remains unchanged.
(3) we can attach just one end of the new wall to an existing pole leaving the other on a new pole. This generates no new rooms, one new pole, and one new wall. So P + R − W again remains unchanged.
We could put the wall up completely separately, but that would be starting a new building.