Brilli's faithfulness for Billi
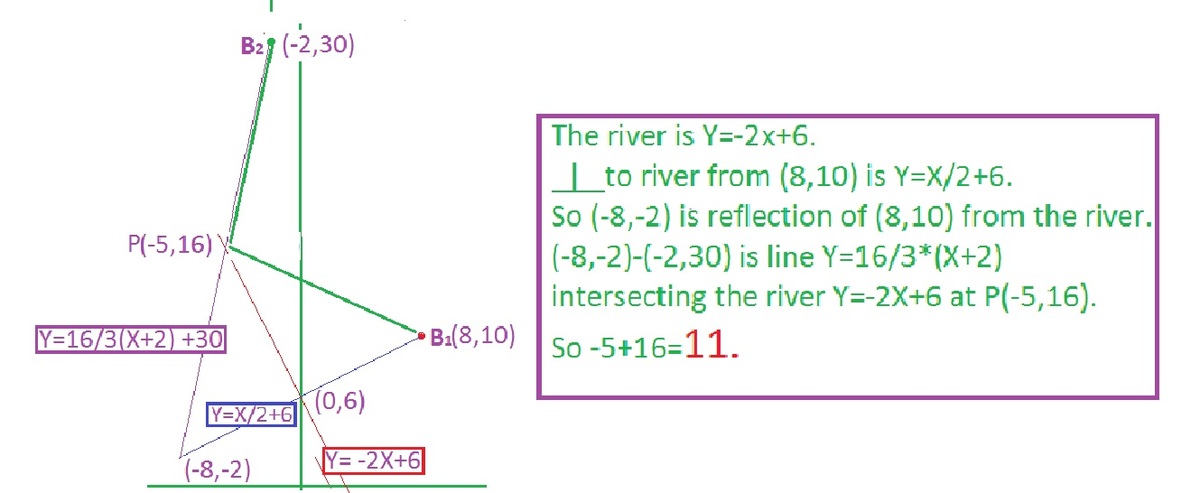
Brilli the ant had his ant hill named which had coordinates .Brilli had his girlfriend named Billi who had her ant hill named which had coordinates . Once Billi was thirsty and she called Brilli to get her some water from a river named Bribill which had equation . Thus to not to displease his girlfriend , Brilli had to take the quickest path which will lead him to Bribill river first and then to Billi's ant hill. Brilli calculated a point on the Bribill river such that if he starts from his ant hill , goes to point and then goes to Billi's ant hill , he would have taken the shortest possible path requiring less efforts and time.
Find the sum of the coordinates of point that Brilli calculated.
Details and Assumptions:
-
Assume the ant-hills as points and the river as a "straight" line.
-
Brilli was always perfect in his calculations.
This problem was created by me. Try more of my originals by clicking here .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The shortest distance B 1 P + P B 2 follows the principle of least action. It is that traveled by light from point B 1 to point P and then reflected at point P (as if the straight-line ( 2 x + y − 6 = 0 ) river is a mirror) to point B 2 .
Let the points where altitudes from B 1 and B 2 meet 2 x + y − 6 = 0 be N 1 and N 2 respectively. Since the angle of incident and angle of reflection is the same, △ B 1 P N 1 and △ B 2 P N 2 are similar and hence, P N 2 P N 1 = B 2 N 2 B 1 N 1 .
Since the river 2 x + y − 6 = 0 ⇒ y = − 2 x + 6 has a gradient of − 2 , lines perpendicular to it must have a gradient of 2 1 . Therefore the equation of B 1 N 1 is given by:
x − 8 y − 1 0 = 2 1 ⇒ y = 2 1 x + 6
The coordinates of N 1 is given by:
y = − 2 x + 6 = 2 1 x + 6 ⇒ x 1 = 0 and y 1 = 6 .
The length of B 1 N 1 = ( 8 − 0 ) 2 + ( 1 0 − 6 ) 2 = 8 0
Similarly, B 2 N 2 : x + 2 y − 3 0 = 2 1 ⇒ y = 2 1 x + 3 1
The coordinates of N 2 : y = − 2 x + 6 = 2 1 x + 3 1 ⇒ x 2 = − 1 0 and y 2 = 2 6 .
The length of B 2 N 2 = ( − 2 + 1 0 ) 2 + ( 3 0 − 2 6 ) 2 = 8 0
Since B 1 N 1 = B 2 N 2 ⇒ P N 1 = P N 2 and P is midway between N 1 and N 2 and its coordinates:
x P = 2 x 1 + x 2 = 2 0 − 1 0 = − 5 y P = 2 y 1 + y 2 = 2 6 + 2 6 = 1 6
⇒ x P + y P = − 5 + 2 6 = 2 1