Brilli's triangular search
Brilli the ant is on a search for food to bring back to his anthill. He starts his search from a point one space above a lattice in the shape of an equilateral triangle with side length 96. A similar lattice is shown in the picture, but this lattice has side length 4.
He searches the lattice by checking each point for food, and then moving to the next point on the lattice. He moves in a zig-zag pattern as shown in the picture. Once he finds food, he goes back to the starting point along the shortest lattice path that he can find.
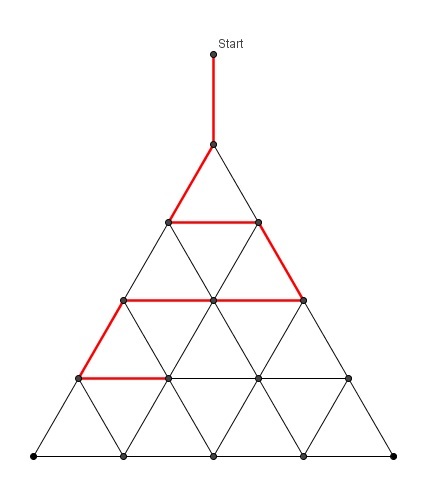
If there is exactly one point in the triangular lattice that contains food, and each point has equal chance of containing food, then what is the expected value of the distance of Brilli's journey?
Notes and clarifications: The starting point will not contain food. When Brilli moves back to the starting point, he moves along the lattice points (not in a straight line to the starting point), but he does not have to retrace the path he used to get to the food.
The answer is 2442.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let's consider a triangle with side lenght n . Let's define the number of layers l = n + 1 . So, the total number of points is p = 2 l ( l + 1 ) . Let's label each point i , 1 ≤ i ≤ p in this way: the point on the summit is i = 1 , the next point Brilli will visit is i = 2 , the adjacent one will be i = 3 and so on. Hence, the total distance travelled if Brilli finds food on point i is
d i = i + l i
where l i is the layer point i is on. Since the probability is uniformly distributed, we have P ( d i ) = p 1 . Hence,
E [ d ] = p 1 i = 1 ∑ p ( i + l i ) = p 1 ( i = 1 ∑ p i + i = 1 ∑ p l i ) = p 1 ( 2 p ( p + 1 ) + i = 1 ∑ p l i )
Notice that there is 1 point on layer l = 1 , 2 on layer l = 2 , 3 on layer l = 3 and so on, so
i = 1 ∑ p l i = k = 1 ∑ l k 2 = 6 l ( l + 1 ) ( 2 l + 1 )
and
E [ d ] = 2 p + 1 + 6 p l ( l + 1 ) ( 2 l + 1 )
Eventually, for our case n = 9 6 , l = 9 7 , p = 4 7 5 3 , so that
E [ d ] = 2 4 7 5 3 + 1 + 6 ⋅ 4 7 5 3 9 7 ( 9 7 + 1 ) ( 2 ⋅ 9 7 + 1 ) = 2 4 4 2
I'll give my solution as a general case for a triangle with side length n .
Define the triangle as a series of rows. Then there are ( n + 1 ) rows in the triangle. The first row has one point, and each subsequent row has one more point. Thus, the number of points in the lattice (not including the starting point) is the ( n + 1 ) t h triangular number: 2 ( n + 1 ) ( n + 2 ) . Therefore, the probability of having food for each point is ( n + 1 ) ( n + 2 ) 2 .
Note that if Brilli gets to a point on the k t h row, then he has exactly k spaces to get back to the starting point.
There are k points in the k t h row, so the probability of finding food in the k t h row is ( n + 1 ) ( n + 2 ) 2 k
Let's first find the distance to get to a point in the k t h row. The distance to get to the last point in the ( k − 1 ) t h row is the ( k − 1 ) t h triangular number: 2 k ( k − 1 ) . From there, to get to any point on the k t h row, Brilli goes a distance anywhere from 1 to k . Because each point on that row has the same probability of having food, we can simplify things by using the average distance between 1 and k : 2 k + 1 .
Thus, the total average distance of Brilli's journey if he finds food on the k t h row is 2 k ( k − 1 ) + 2 k + 1 + k = 2 k 2 + 2 k + 1
Using the probability for the k t h row from before, the expected value of Brilli's journey is: ( n + 1 ) ( n + 2 ) 1 k = 1 ∑ n + 1 ( k 3 + 2 k 2 + k )
= ( n + 1 ) ( n + 2 ) 1 [ k = 1 ∑ n + 1 k 3 + 2 k = 1 ∑ n + 1 k 2 + k = 1 ∑ n + 1 k ]
= ( n + 1 ) ( n + 2 ) 1 [ 4 ( n + 1 ) 2 ( n + 2 ) 2 + 6 2 ( n + 1 ) ( n + 2 ) ( 2 n + 3 ) + 2 ( n + 1 ) ( n + 2 ) ]
= 4 ( n + 1 ) ( n + 2 ) + 3 2 n + 3 + 2 1
= 1 2 3 n 2 + 1 7 n + 2 4
With n = 9 6 , this expression evaluates to 2 4 4 2 .
I'd be interested in seeing if anyone comes up with a simpler solution. Also potentially interesting: is it possible for Brilli to take a path that would result in a lower expected distance?
Split up the route into outgoing and returning portions.
Outgoing: Each of the distances 1 , 2 , . . . , 4 7 5 3 is equally likely. so the expected outgoing distance is 4 7 5 3 1 + 2 + ⋯ + 4 7 5 3 = 2 4 7 5 4 = 2 3 7 7 .
Returning: Returning from each of the k points on the k th level gives a distance of k , so the expected returning distance is 4 7 5 3 1 2 + 2 2 + ⋯ + 9 7 2 = 3 1 9 5 = 6 5 .
Thus, the total expected distance is 2 3 7 7 + 6 5 = 2 4 4 2 .
In general, this works out to 4 ( n + 1 ) ( n + 2 ) + 2 + 3 2 n + 3 = 1 2 3 n 2 + 1 7 n + 2 4