Broken Pinwheel
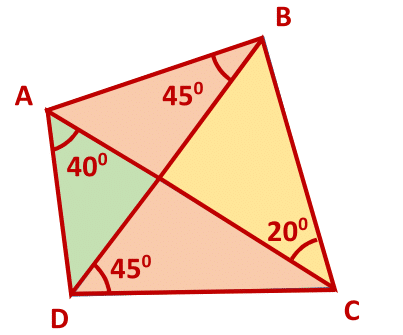
In a quadrilateral let , , and Find the smaller of the two angles between the diagonals.
Report the average of the solutions to this problem to four decimal places.
Note: The image provided is not to scale.
The answer is 58.4333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The sides AB and CD of the quadrilateral have to be parallel, since ∠ A B D = ∠ B D C . We can set the distance between the lines to 1. Let's name the ∠ B A C = ∠ A C D = x . This has to satisfy the equation
cot ( x + 4 0 ∘ ) + 1 + cot ( x + 2 0 ∘ ) = cot ( x )
Using the identity for a cotangent of a sum, we get
cot ( x ) − 1 = cot ( 4 0 ∘ ) + cot ( x ) cot ( 4 0 ∘ ) × cot ( x ) − 1 + cot ( 2 0 ∘ ) + cot ( x ) cot ( 2 0 ∘ ) × cot ( x ) − 1
This is a third degree equation in cot ( x ) with three solutions:
cot ( x 1 ) = 2 . 7 8 5 8 , x 1 = 1 9 . 7 4 6 3 ∘ , which corresponds to an angle between diagonals of 6 4 . 7 4 6 3 ∘ .
cot ( x 2 ) = 0 . 1 2 4 9 , x 2 = 8 2 . 8 7 9 7 ∘ , which corresponds to an angle between diagonals of 5 2 . 1 2 0 3 ∘ .
and finally cot ( x 3 ) = − 1 . 9 0 7 1 , x 3 = 1 1 7 . 6 7 0 1 ∘ .
This configuration, however, does not give a quadrilateral with desired properties and is therefore not a valid solution.