Broken tree
During the hurricane a 16-meter-tall tree got fractured and its higher part fell down so that its tip touched the ground at the distance of 8 meters from the trunk. At what height is the fracture?
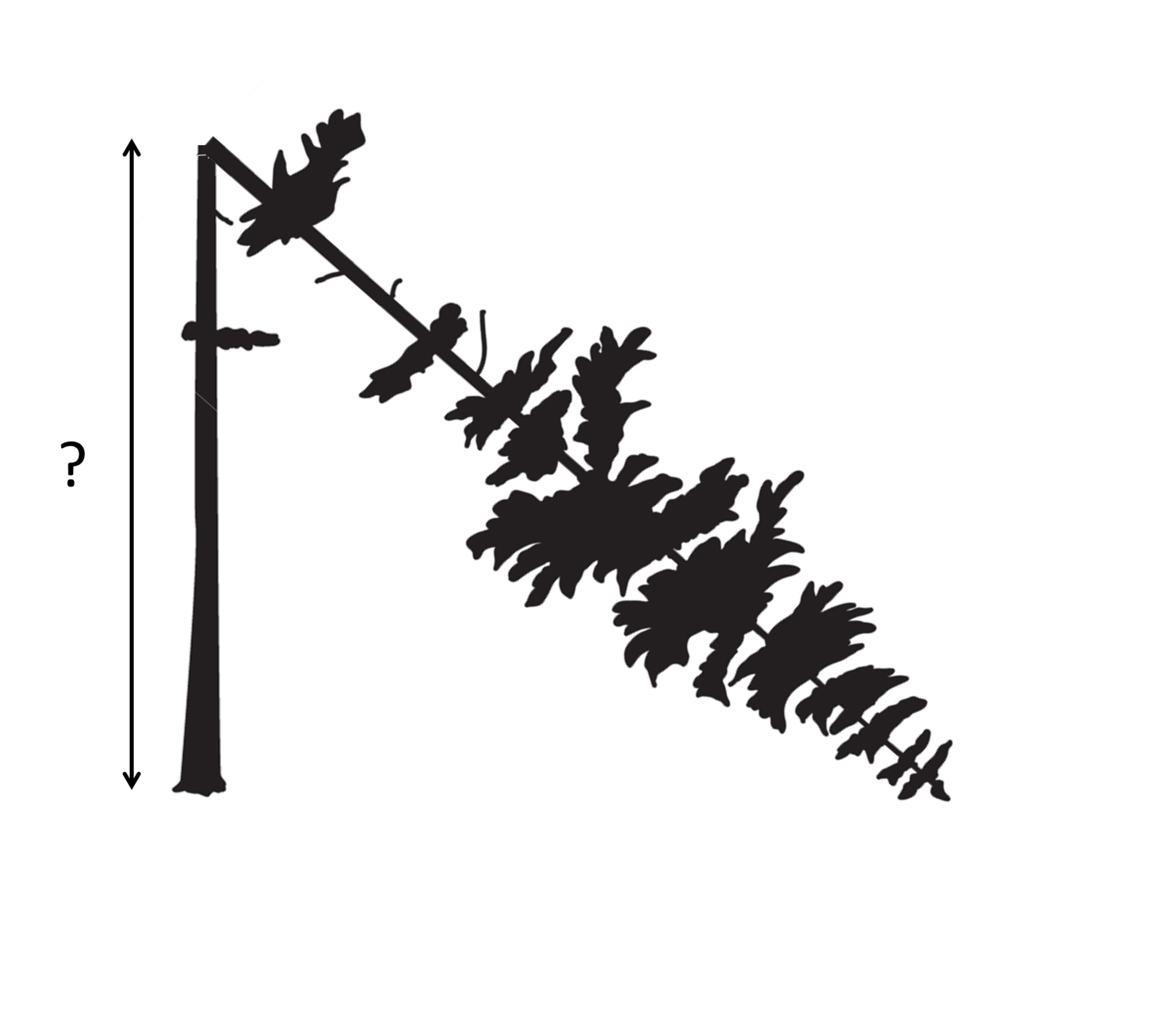
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I would urge caution when combining a ruler-and-compass construction with a distance estimation.
The task comes from a text book for mathematics in fifth grade (I only changed the numbers to get an integer as a solution). It appears that the pupils learn ruler-and-compass construction first, before they get to know Pythagorean theorem. This is actually the reason why I have made the construction to find a solution. I think it is an interesting approach too, so I wanted to show it.
Say the fracture is at a height h from the ground. The length of the broken top part of the tree is 1 6 − h . By Pythagoras, h 2 + 8 2 = ( 1 6 − h ) 2
Expanding, h 2 + 6 4 = 2 5 6 − 3 2 h + h 2
Cancelling and rearranging, 3 2 h = 1 9 2
Solving, h = 6
Did it the same way.
I solved the task using ruler-and-compass construction. I am going to show the steps below: 1. This is the initial problem: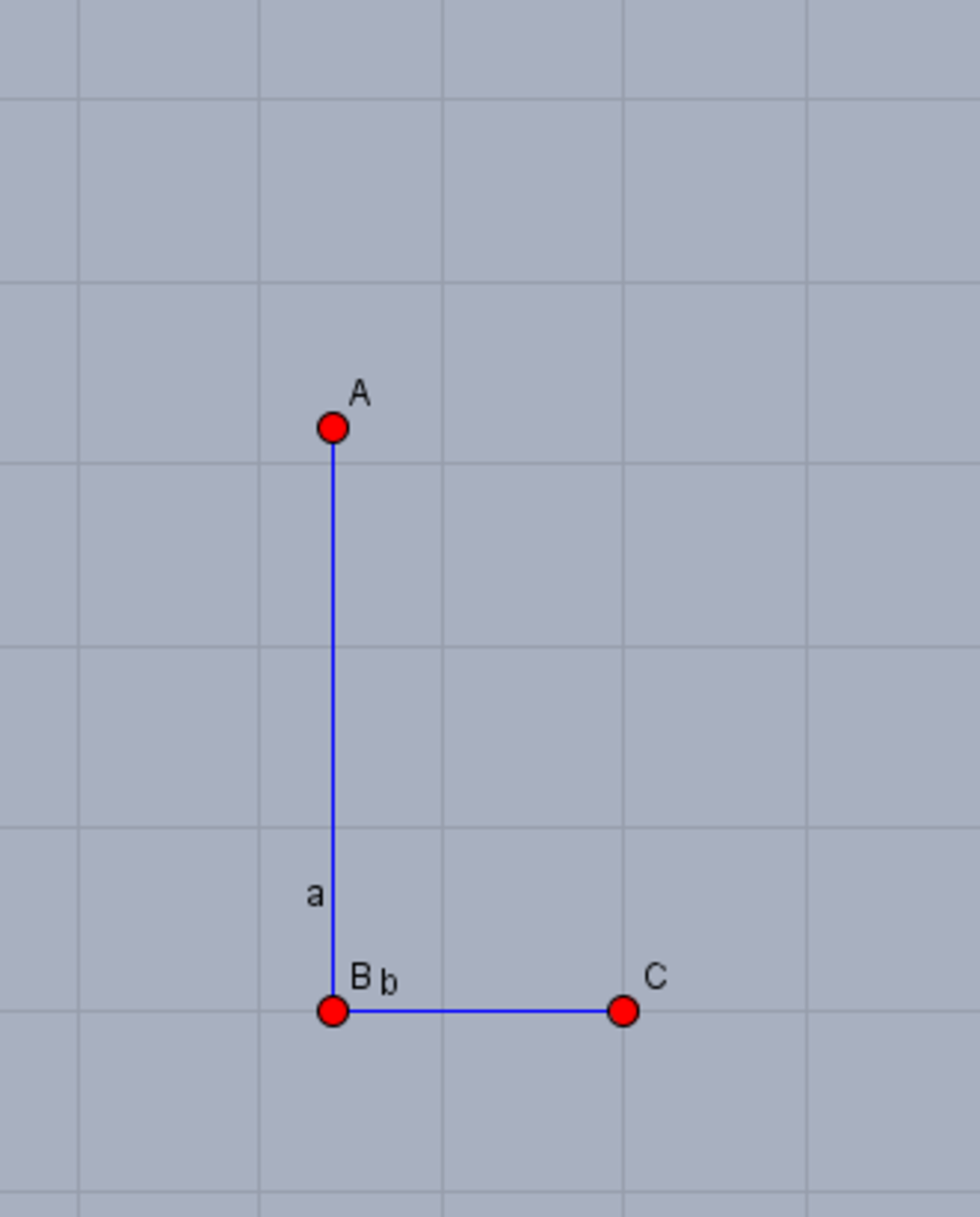 2. Draw circles of the same radius and the centers of points A and C, so that the circles intersect:
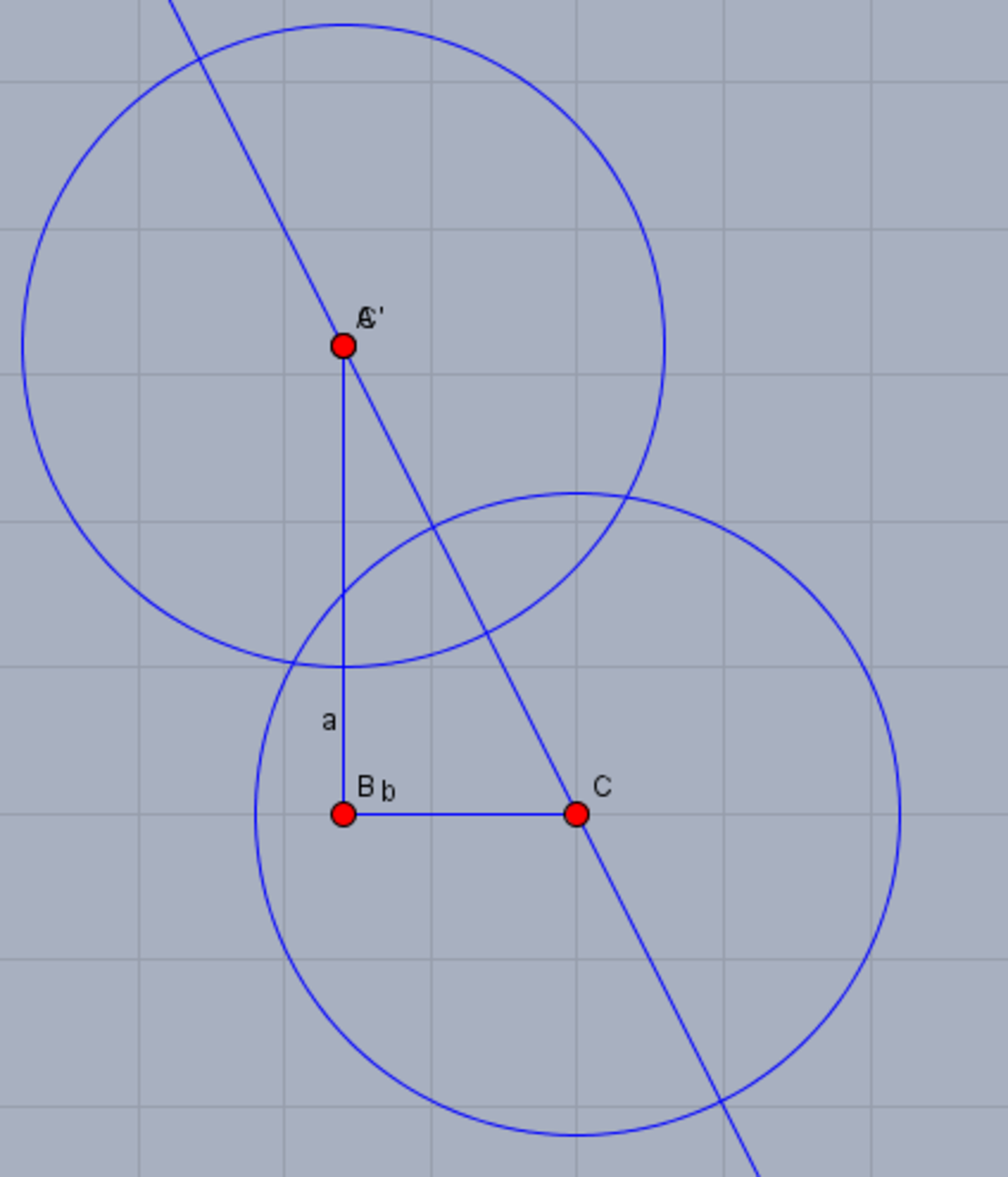
2. Draw circles of the same radius and the centers of points A and C, so that the circles intersect:
 3. Connect the points D and E. The segment DE is a bisector of the line segment AC
3. Connect the points D and E. The segment DE is a bisector of the line segment AC
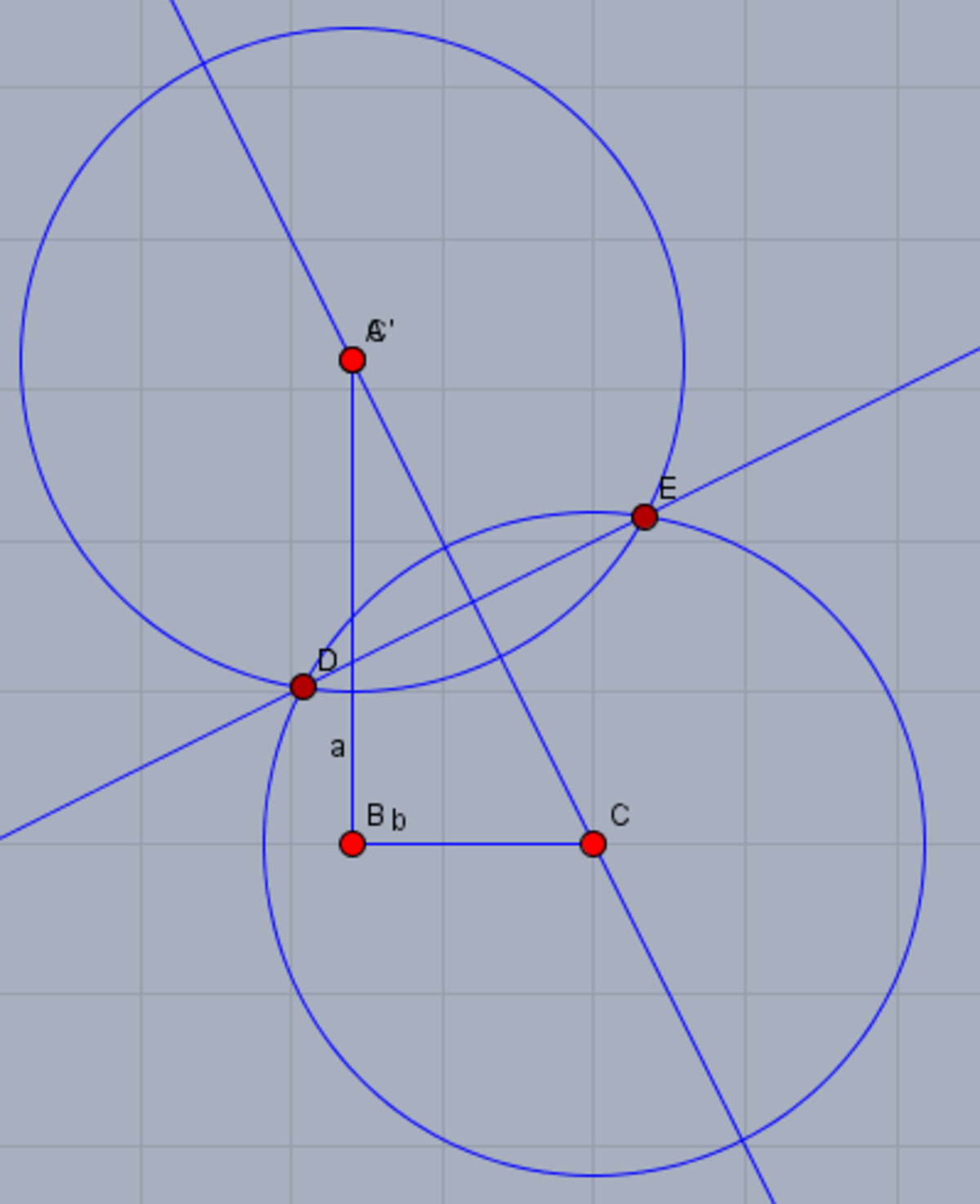 4. The searched height is the segment BF, wchich is 6 units long:
4. The searched height is the segment BF, wchich is 6 units long:
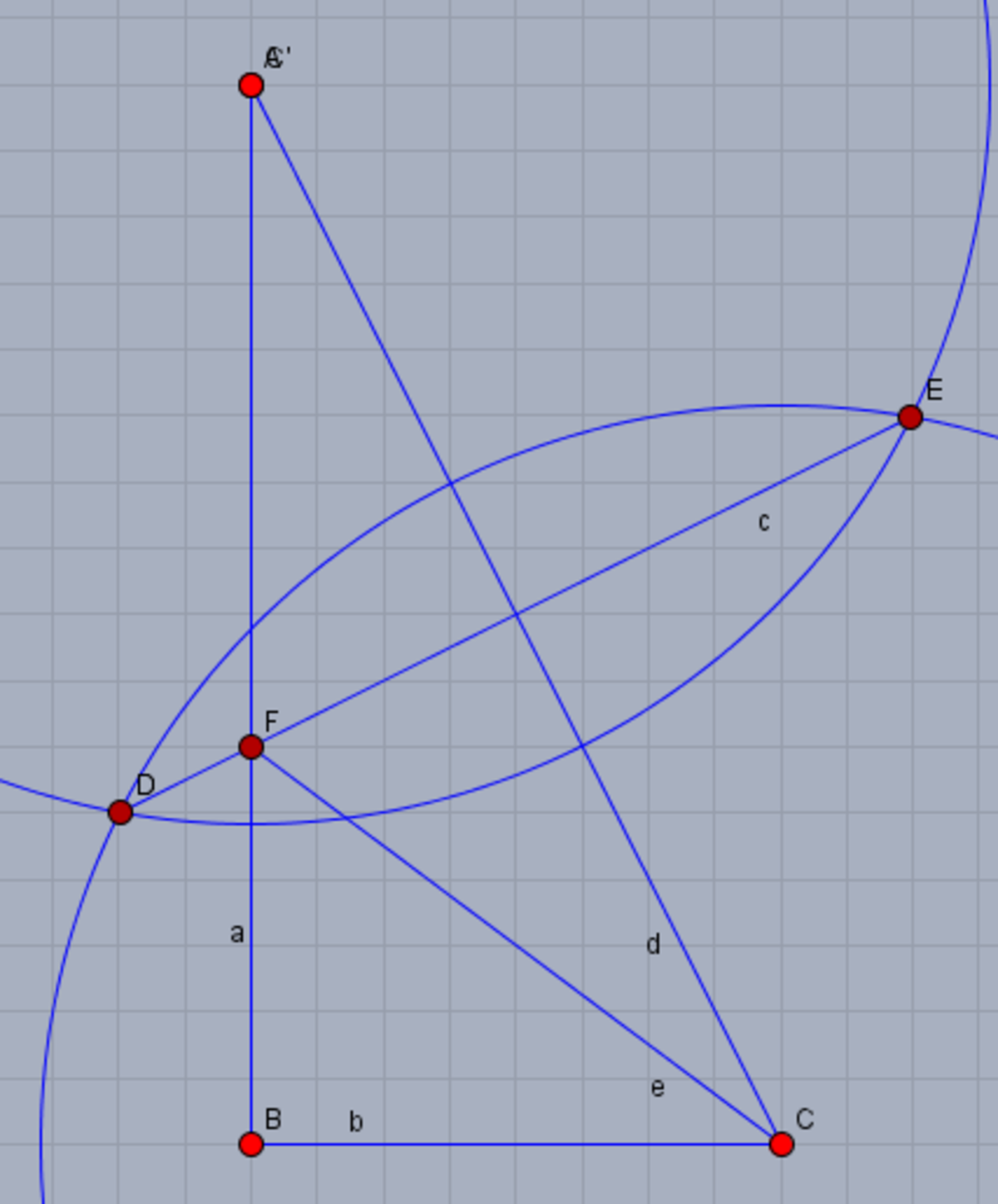 It is so because the segments AF and CF have equal length, which sum up to the initial height of the tree.
It is so because the segments AF and CF have equal length, which sum up to the initial height of the tree.