Broken Vase
Mother came home and saw a broken vase. She immediately questioned her 4 children, who replied as follows:
Alex: "It wasn't Brian. It was Daniel."
Brian: "It wasn't Charlie. It wasn't Daniel."
Charlie: "It wasn't Daniel. It was Brian."
Daniel: "It was Charlie. It was Brian."
It is known that each of them told one true and one false statement. Who broke the vase?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Moderator note:
While listing all the cases can often solve a logic problem like this, some simple deduction can make life simpler. For example, we know from Daniel's statements and the fact one of them is true that either Brian or Charlie broke the vase, so we didn't need to test the cases of Alex or Daniel breaking the vase.
Also of note: Daniel's statements + the statements of any one of the other people are sufficient to find who broke the vase.
Very systematic and elegantly presented!
Doing a case study on each child being the culprit proves the validity of the problem and its available answers - It isn't overkill to any degree.
If there are multiple cases that satisfy the requirement for "one true and one false statement", then the problem is invalid.
Yes I agree, Brian's solution is simpler and requires less work. It's nice to see all possible outcomes anyway though.
Trying out mental science of deduction method- I see the point of confirming Alex did not break the vase, as he was not mentioned at all. But what about Daniel?!
Log in to reply
2nd deduction, Brian mentioned it was neither Charlie and Daniel. So we can strike off Brian, as it has to be Charlie or Daniel.
Final deduction, Daniel's statement implied it was either Charlie or Brian. And we obviously know it can't be Brian. Hence, Charlie was the culprit who broke the vase
As challenge master notes, the exhaustive demonstration is massive overkill.
Every statement of the form "It was" - "It wasn't: is automatically true on the "wasn't" side, because otherwise both would be true.
That heads us straight to the single "It was"-"It was" statement where one of the statements is known false from one of the "was"-"wasn't" statements, forcing the other state to be true and directly identify the culprit.
Two steps.
Since one of Brian's statements is true the culprit must be one of either Charlie or Daniel, and since one of Daniel's statements is true the culprit must be one of Charlie or Brian. The intersection is Charlie. Alex and Charlie, whose statements are logically identical, with Charlie as the culprit, each make one true statement, ("It wasn't Brian"), and one false statement, ("It was Daniel"). Thus all their replies are consistent with Charlie being the one who broke the vase.
Nice analysis! Looks like you didn't break the vase ;)
Log in to reply
Hahaha Yeah, I never did trust Charlie, but I wasn't going to snitch on him. :)
You only need Daniel and Brian's statements to solve this one. Start with Daniel's statement: "It was Charlie. It was Brian." One is true, so we know Alex and Daniel are innocent. Now, Brian's statement: "It was not Charlie. It was not Daniel." We already know Daniel is innocent, so the second part of Brian's statement is true. Therefore, "It was not Charlie" is false- so it WAS charlie. You can double check Alex and Charlie's statements. They check out.
@Jerry Goldin interesting point! (However, I believe you CAN assume that only 1 is guilty because the only choices given are singular names.)
You would be wrong. You are assuming only one person is guilty, but the problem doesn't state that. All you can gather from Daniel's statement by itself is that either Charlie or Brian was involved but not both.
This can be solved from Alex and Brian's statements:
If it was Daniel, then both of Alex's statements are true. So it can't be Daniel. Brian says it wasn't Daniel and it wasn't Charlie. We know the first is true so the 2nd must be false. It was Charlie.
Yep, it is interesting to notice that just two of the statements solve the problem. A good way to start is to notice that there is the pair "It was Daniel" and "It wasn't Daniel.". That helps solving a lot of these problems
All the was-wasn't's are automatically true on the wasn't side, One of them directly triggers the single was-was statement. Gets my vote.
Ah, the good old "laying down all the possible scenarios" always works!
A combination of any two statements can be used to solve this problem, except a combination of Alex's and Charlie's statements (because they both confirm the same two innocent children - which leaves one innocent child and one guilty child in question).
My first instinct was to use Daniel's statement as my lynchpin for this problem, because it directly implicates the guilty child. From there, any other statement confirms that Charlie is guilty.
lynchpin is an interesting word. I had to google it.
A combination of any two statements can be used to solve this problem, except a combination of Alex's and Charlie's statements (because they both confirm the same two innocent children - which leaves one innocent child and one guilty child in question).
That is a rather remarkable observation. It's almost like four people know the coordinates of their points on a line but at least two of them need to cooperate to get the equation of the line.
Log in to reply
It's not a perfect use of the word ' lynchpin ', but it is a nice word, and fits well enough.
For my own obsession with this problem being universally solved with only two statements, I would have preferred that the children's replies were:
Alex : "It wasn't Brian. It was Daniel."
Brian : "It wasn't Charlie. It wasn't Alex ."
Charlie : "It wasn't Daniel. It was Alex ."
Daniel : "It was Charlie. It was Brian."
It isn't necessary for Brian's reply to be updated to say "It wasn't Alex." instead of "It wasn't Daniel." to satisfy a 'universal two statement solution', but it fulfils an additional obsession of mine for even distribution.
Since we know that everybody says one true and one false statement. If you say a combo as: "it was A", "it wasn't B". We know that "it was A" must be the lie. If "it was A" was the truth it means it "it wasn't B" was the lie so that statement would become "it was A", "it was B" which can't be
Thus we know for a fact from Alex & Charlie: It wasn't neither Brian, nor Daniel
By looking at either Charlie or Daniel we can correct their statement to
Brian: "It was Charlie. It wasn't Daniel." (we know Daniel can't be per above)
Daniel: "It was Charlie. It was Brian." (We know Brian can't be per above)
Oh, nice observation, Diego! From Alex's statement alone we can determine that the culprit was neither Brian nor Daniel. Charlie's statement then does not give us any extra information.
Brian says it wasn't Charlie and It wasn't Daniel, one of which is a lie. So it is either Charlie or Daniel.
If it was Daniel, both of Alex's statements become true which is impossible. Therefore it has to be Charlie
Simple trick! was wasn't Daniel Brian Brian +1 Charlie Charlie Daniel +1
No plus in charlie so he must be guilty.
Daniel's answer implies that it must've been either Brian or Charlie. Brian's answer implies that it must've been either Charlie or Daniel. The only way for both of these to be true is for Charlie to have done it.
Yep, this is a great observation. Also notice that the puzzle would be unsolvable if these two sets didn't have a non-empty intersection.
No need for big complicated charts or long explanations. You can get the correct answer from just the last two (Charlie's and Daniel's) statements, no need for the other two. Daniel's statement means that it had to be either Charlie or Brian. If it were Brian, then both of Charlie's statements would be true, so it had to be Charlie.
That is true. But charts really help in solving harder logic puzzles, though.
Just focus on the Daniel's statement.It is clear that it has to be either Charlie or Brian.Now coming on to Charlie's 1st statement,which says "It wasn't Daniel" has to be true because it is either Charlie or Brain.Now Charlie's 2nd statement "It was Brain" has to be false.So the answer is Charlie.
Yep, interestingly just two of the four pairs suffice to solve the problem. Looking at the solution, there are more than just one pair which is sufficient.
Isn't that cool?
Alex's 1st statement can't be false because if it is false, then his 2nd statement will be true. It means both Brian & Daniel broke the vase which is not possible at all. So, Brian's 1st & 2nd statements are false & true respectively and hence Charlie broke the vase.
Yep, it is interesting to notice how just the form of the statements matter and not the names. We could also look at Charlie's Statements.
"It wasn't Daniel. It was Brian."
and go forward.
On a different note, I do not think it is a good idea to use the phrase "Clearly" in the solution here. That makes the entire solution sound like a very trivial piece of work.
First look at Daniel and you will find that it is either Charlie or Brian, which means Alex and Daniel are off the list. We know from Alex that it wasn't Daniel as his false and it wasn't Brian being true. We get Charlie then. It all fits in as well.
Yes, we can find out who the culprit is with just two statements, but it is important to check if others' statements are consistent too.
I added them all together with + and - and charlie came out with 2 strikes.
Can you explain what you mean by added them together and strikes? I am lost here.
Let's run through the outcomes of each child's first and second statements:
Alex broke the vase: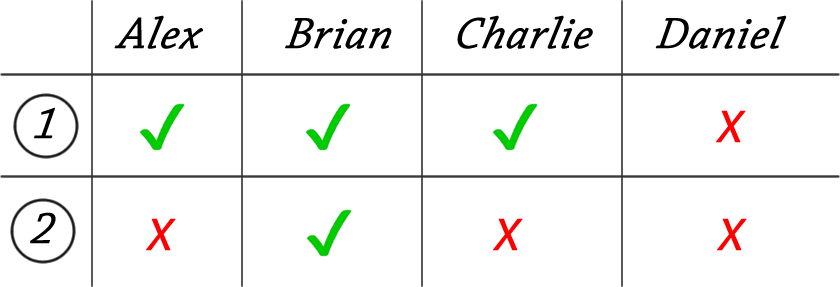
Brian broke the vase: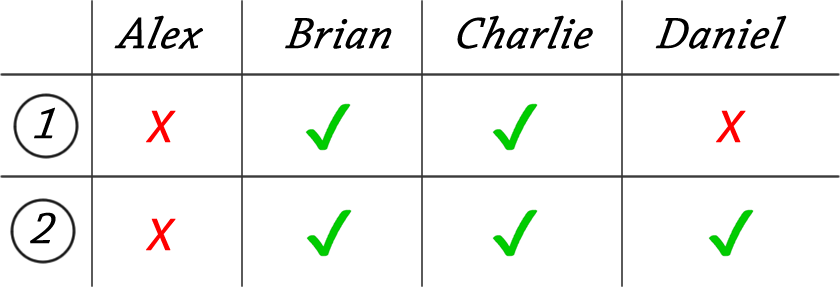
Charlie broke the vase: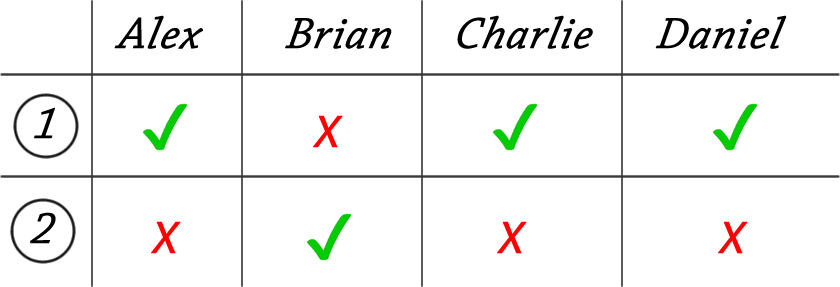
Daniel broke the vase: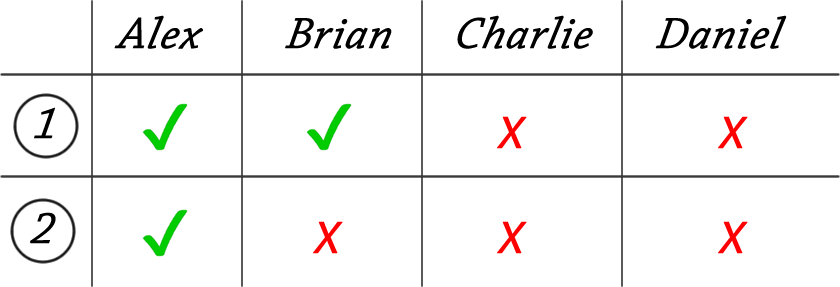
From this we can easily see that, only in the case when the vase is broken by Charlie, each child tells one lie and one truth.
Charlie broke the vase