Brother Brocard's Brilliant Biological Bond
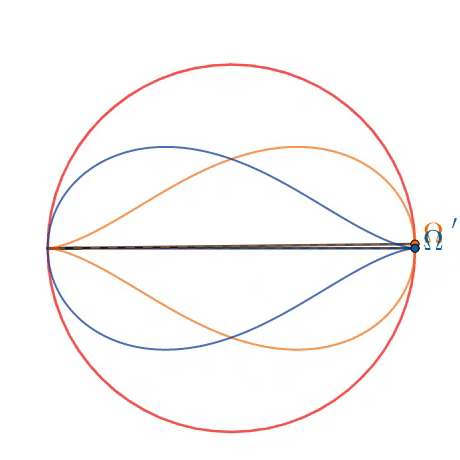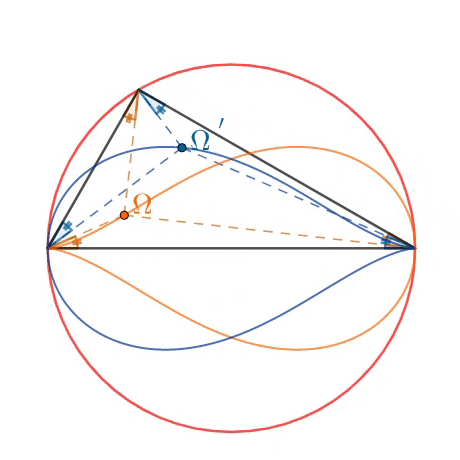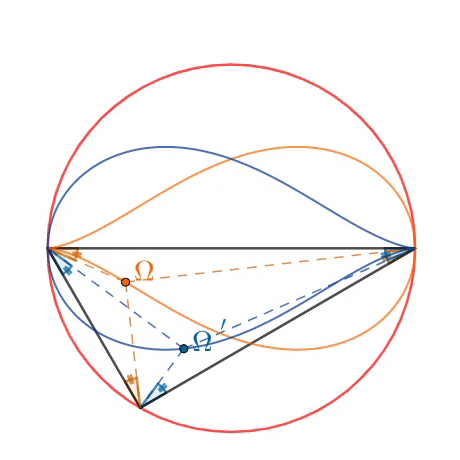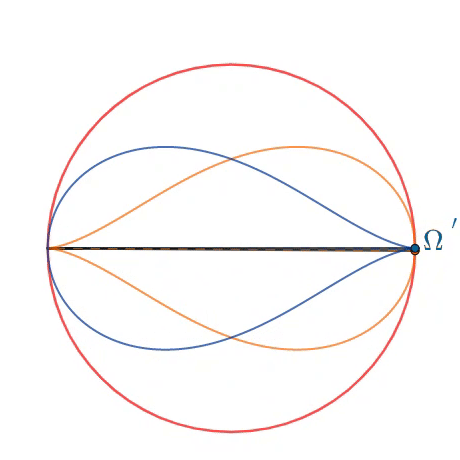
In a unit circle, two fixed endpoints on the diameter and the third point altogether form the triangle. As the third point varies, two loci of Brocard points - Ω (orange) and Ω ′ (blue) - each form the teardrop curve. As shown in the animation, these points are formed by extending three segments, for which all three respective angles are equal with the unique Brocard angle ω .
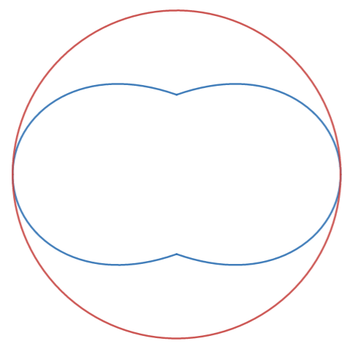
For this problem, find the total largest area enclosed by both curves (above in blue). If the area is A , input ⌊ 1 0 6 A ⌋ as your answer.
The answer is 1881336.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
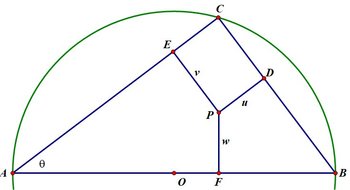 Time for a general approach using trilinear coordinates. Let us set up the (by now) standard angle
θ
=
∠
B
A
C
, so that
A
,
B
,
C
have coordinates
(
−
1
,
0
)
,
(
1
,
0
)
and
(
cos
2
θ
,
sin
2
θ
)
respectively, and so the triangle
A
B
C
has sides
a
=
2
sin
θ
,
b
=
2
cos
θ
,
c
=
2
. Consider a point
P
which has exact trilinear coordinates
u
:
v
:
w
, so that
u
,
v
,
w
are the perpendicular distances from
P
to the sides
B
C
,
A
C
,
A
B
respectively. We note that
2
1
(
a
u
+
b
v
+
c
w
)
=
Δ
, the area of
A
B
C
, and hence
u
sin
θ
+
v
cos
θ
+
w
=
sin
2
θ
Since
C
D
P
E
is a rectangle, we deduce that
O
P
=
O
C
−
u
(
sin
θ
cos
θ
)
+
v
(
−
cos
θ
sin
θ
)
and hence
P
has coordinates
(
X
(
θ
)
,
Y
(
θ
)
)
=
(
cos
2
θ
−
u
cos
θ
+
v
sin
θ
,
w
)
The two Brocard points
Ω
and
Ω
′
have relative trilinear coordinates
b
c
:
c
a
:
a
b
c
b
:
a
c
:
b
a
respectively, and so
Ω
has coordinates
(
X
(
θ
)
,
Y
(
θ
)
)
=
(
9
−
cos
4
θ
8
(
cos
4
θ
+
cos
2
θ
−
1
)
,
9
−
cos
4
θ
1
6
sin
θ
cos
3
θ
)
Time for a general approach using trilinear coordinates. Let us set up the (by now) standard angle
θ
=
∠
B
A
C
, so that
A
,
B
,
C
have coordinates
(
−
1
,
0
)
,
(
1
,
0
)
and
(
cos
2
θ
,
sin
2
θ
)
respectively, and so the triangle
A
B
C
has sides
a
=
2
sin
θ
,
b
=
2
cos
θ
,
c
=
2
. Consider a point
P
which has exact trilinear coordinates
u
:
v
:
w
, so that
u
,
v
,
w
are the perpendicular distances from
P
to the sides
B
C
,
A
C
,
A
B
respectively. We note that
2
1
(
a
u
+
b
v
+
c
w
)
=
Δ
, the area of
A
B
C
, and hence
u
sin
θ
+
v
cos
θ
+
w
=
sin
2
θ
Since
C
D
P
E
is a rectangle, we deduce that
O
P
=
O
C
−
u
(
sin
θ
cos
θ
)
+
v
(
−
cos
θ
sin
θ
)
and hence
P
has coordinates
(
X
(
θ
)
,
Y
(
θ
)
)
=
(
cos
2
θ
−
u
cos
θ
+
v
sin
θ
,
w
)
The two Brocard points
Ω
and
Ω
′
have relative trilinear coordinates
b
c
:
c
a
:
a
b
c
b
:
a
c
:
b
a
respectively, and so
Ω
has coordinates
(
X
(
θ
)
,
Y
(
θ
)
)
=
(
9
−
cos
4
θ
8
(
cos
4
θ
+
cos
2
θ
−
1
)
,
9
−
cos
4
θ
1
6
sin
θ
cos
3
θ
)
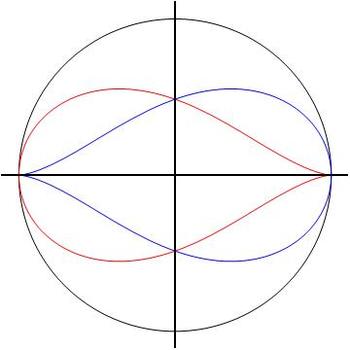 The loci of
Ω
and
Ω
′
are shown in blue and purple respectively here. The locus of
Ω
′
is the reflection of the locus of
Ω
in the
y
-axis. Thus the desired area is equal to
4
times the area of the interior of the locus of
Ω
that lies in the first quadrant. Thus we want to calculate
A
=
4
∫
θ
0
0
X
′
(
θ
)
Y
(
θ
)
d
θ
=
2
0
4
8
∫
0
θ
0
(
9
−
cos
4
θ
)
3
cos
4
θ
(
1
1
+
4
cos
2
θ
+
cos
4
θ
)
sin
2
θ
d
θ
where
θ
0
=
cos
−
1
2
1
(
5
−
1
)
is the value of the parameter
θ
where the locus of
Ω
meets the positive
y
-axis. A
t
=
tan
θ
substitution, followed by partial fractions, will handle this integral, and we obtain
A
=
5
1
[
5
2
(
5
−
1
)
−
1
0
tan
−
1
5
−
2
+
2
5
tan
−
1
5
(
2
+
5
)
]
and hence
⌊
1
0
6
A
⌋
=
1
8
8
1
3
3
6
.
The loci of
Ω
and
Ω
′
are shown in blue and purple respectively here. The locus of
Ω
′
is the reflection of the locus of
Ω
in the
y
-axis. Thus the desired area is equal to
4
times the area of the interior of the locus of
Ω
that lies in the first quadrant. Thus we want to calculate
A
=
4
∫
θ
0
0
X
′
(
θ
)
Y
(
θ
)
d
θ
=
2
0
4
8
∫
0
θ
0
(
9
−
cos
4
θ
)
3
cos
4
θ
(
1
1
+
4
cos
2
θ
+
cos
4
θ
)
sin
2
θ
d
θ
where
θ
0
=
cos
−
1
2
1
(
5
−
1
)
is the value of the parameter
θ
where the locus of
Ω
meets the positive
y
-axis. A
t
=
tan
θ
substitution, followed by partial fractions, will handle this integral, and we obtain
A
=
5
1
[
5
2
(
5
−
1
)
−
1
0
tan
−
1
5
−
2
+
2
5
tan
−
1
5
(
2
+
5
)
]
and hence
⌊
1
0
6
A
⌋
=
1
8
8
1
3
3
6
.