Bubbles in a web
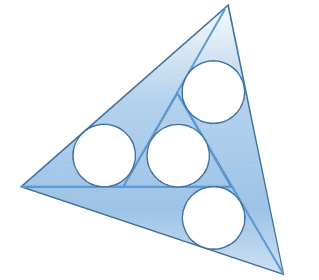 Four identical circles are inscribed into a web of four triangles inside an equilateral triangle with side length 1, as shown in the diagram. Find the radius of the circles to 3 decimal places.
Four identical circles are inscribed into a web of four triangles inside an equilateral triangle with side length 1, as shown in the diagram. Find the radius of the circles to 3 decimal places.
The answer is 0.114.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The three triangles on the outside are all congruent. We will get an expression for the radius R of the inscribed circle from R × s = A where s is half perimeter and A is area.
We can introduce x = A B = C D . This will give us the area as A = 2 1 x ( 1 + x ) × s i n ( 1 2 0 ∘ ) = 4 3 x ( x + 1 ) .
To get circumference we need y , which can be obtained from the law of cosines as y = x 2 + ( 1 + x ) 2 − 2 1 x ( x + 1 ) × c o s ( 1 2 0 ∘ ) .
R × s = A will now become 3 1 × ( x + ( x + 1 ) + y ) = 4 3 x ( x + 1 )
This has only one applicable solution, namely x = 0 . 9 3 0 4 3 , which corresponds to y = A D = 2 . 5 2 7 5 .
We were supposed to have y = 1 , so all the results need to be scaled down to that, with the radius becoming R = 2 3 1 × y 1 = 0 . 1 1 4 2