Building a cone of maximum volume
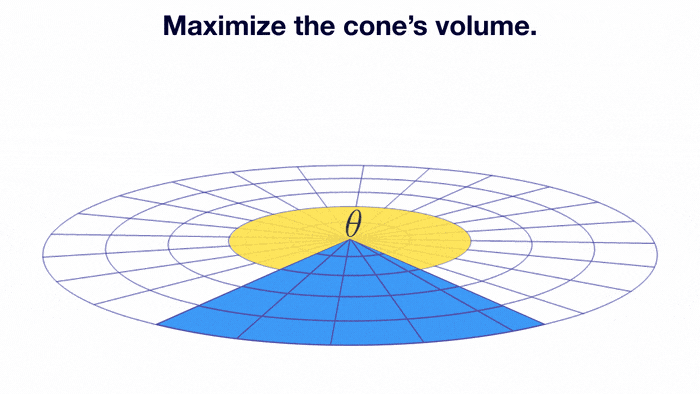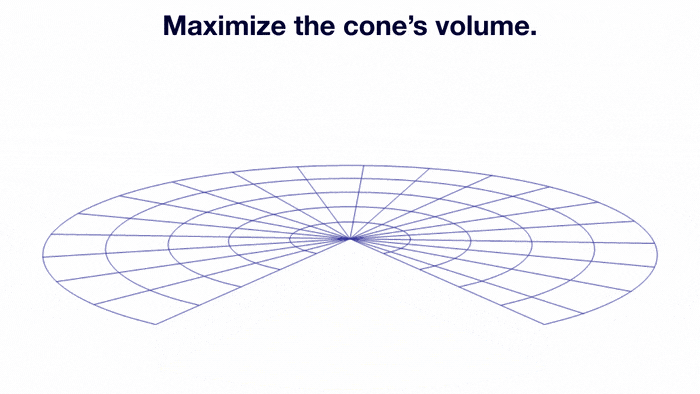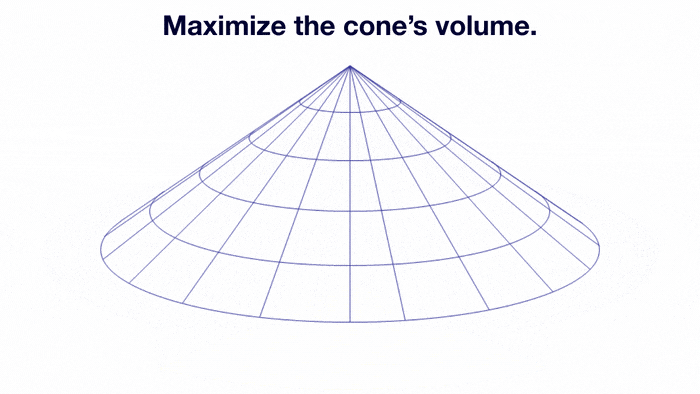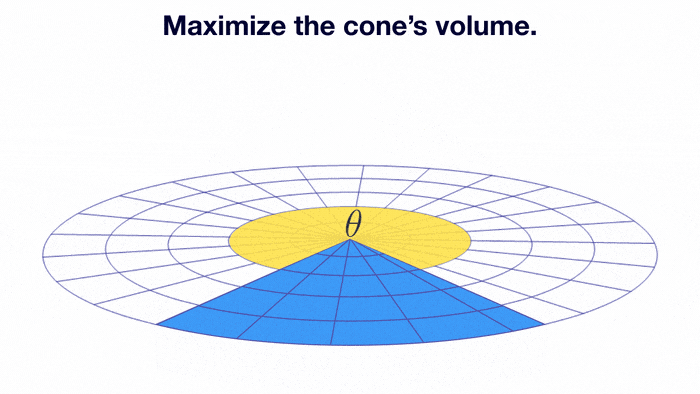
Let's make a cone out of a circular piece of paper.
We first cut out a sector, and connect the radius in the remaining sector, as demonstrated by the animation.
To maximize the volume of the resultant cone, what must be the central angle (in degrees, to 2 decimal places) of the remaining sector?
The answer is 293.94.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Did exactly the same way! Nice problem sir.
Also did it the exact same way in the end, but I had the misfortune of finding the wrong way twice (once I forgot to square the theta*pi in the denominator of h; second time I tried solving it through by converting to degrees first) because I didn't go for the elegant substitution.
Square f(x) and then take derivative would be easier ,btw same method.
A nice solution. Once I had f(x) by the same reasoning as yourself I differentiated wrt x 2 . It makes the calculation marginally easier.
First of all, you can NEVER come up with a cone by cutting a sector of a circle, because a sectioned verge of a circle will not make a circle when you unite the parts together. I practiced it. It results a deformed circle, not inscribed in a plane.
Log in to reply
I agree. It is actually true that a surface of a cone has positive curvature, the circle has 0.
That depends on the materials you're using to build the surface of the cone. But in theory, you should get a cone by folding a circular sector.
Like other have pointed out. It's certainly easier to find the solution of f ′ ( x ) = 0 if we consider ( f ( x ) ) 2 instead.
It's nice that there isn't a need to use the second derivative test to prove the maximality....
It is easy to see, that the size of radius of the original circle shape (s, also the slant height of the cone) does not influence the size of the residual central angle of the cone with the maximal volume (this is due to similarity).
Let s = 1
(We could use this method as well when calculating lengths/areas/volumes with parameters or actual values, by using an enlargement, scale factor = s).
Then, we can take the (well known) right angled triangle formed by the radius of the base circle of the cone (r), the height of the cone (h) and the slant height of the cone (s = 1, hypotenuse) and apply Pythagoras' theorem:
r 2 = 1 − h 2
The volume of the cone:
V = 3 π r 2 h = 3 π ( 1 − h 2 ) h = 3 π ( h − h 3 ) → max
The first derivative of V:
3 π ( 1 − 3 h 2 ) = 0
1 − 3 h 2 = 0
Since h is a height, h > 0:
h = 3 1
And it is easy to see from the second derivative of V, that this is really a maximum as:
V ′ ′ = 3 π ( 1 − 6 h ) = 3 π ( 1 − 2 3 ) < 0
Then:
r = 3 2
The residual central angle, x can be calculated by using the ratio between the circumferences of the original circle and the base circle of the cone (which is the same as the ratio of their radii, r and s (= 1)):
x = s r × 3 6 0 ° = 3 2 × 3 6 0 ° = 2 9 3 . 9 4 ° (2 d. p.)
Yes, this looks like a viable calculus approach. Most users often neglect to prove that its second derivative is negative. But is there an alternative approach where we don't have to show use the second derivative test but still manage to prove that the critical point is maximum?
On the other hand, I was thinking about whether we can show that volume is maximized when r : h = 2 : 1 via some classical inequalities, but that has still alluded me.... Thoughts?
Log in to reply
It's kind of hard to think of a "geometrical explanation" that's even simpler than to ask the question, for which altitude h is the following expression the maximum?
V = k h ( 1 − h 2 )
which immediately gets us h = 3 1
Log in to reply
Ah, fair enough. Maybe I was just trying to think of a convoluted method to solve this rather straightforward question...
Since this is under the calculus section, i challenged myself to do this without looking up the volume of a cone, i did the following: Let the angle be theta, let the radius of the circle be a constant. The radius of the bottom section of the cone must then be
R ( θ ) = r ⋅ 3 6 0 θ
We can now imagine we have a triangle where the height of the cone is the base, the radius of the original circle is the hypothenuse, and the radius of the bottom of the cone is the last cathetus.
We can then find the height by using the pythagorean theorem
h ( θ ) = r 2 − R 2 ( θ )
If we now want a linear function that follows the edge of the cone, it must be
f ( x , θ ) = h ( θ ) R ( θ ) ∗ x
The volume of the cone must then be a volume of revolution, given by
V ( θ ) = 2 π ⋅ ∫ 0 h ( θ ) f 2 ( x , θ ) d x
We can now solve for
V ′ ( θ ) = 0
If we discard the 0, we find a maximum at 293.94
Oh woaah, I never thought we can avoid the formula of cone volume and still manage to pull this off.
Let me see if I can do the same trick for other optimization problems tooo~
Let s be the radius of the circle, and ϕ the angle of the sector to be folded. Upon folding, the radius of the base r is related to s and ϕ by
r = s 2 π ϕ
and therefore, the height of the cone will be h = s 2 − r 2 = s 1 − ( 2 π ϕ ) 2
It follows that the volume of the cone is
V = 3 1 π s 3 ( 2 π ϕ ) 2 1 − ( 2 π ϕ ) 2
Let x = 2 π ϕ , then we want to maximize
f ( x ) = x 2 1 − x 2
The derivative is given by
f ′ ( x ) = 2 x ( 1 − x 2 ) 1 / 2 − x 3 ( 1 − x 2 ) − 1 / 2 = ( 1 − x 2 ) − 1 / 2 ( 2 x − 3 x 3 )
f ′ ( x ) = 0 implies x = 0 or x = 3 2
x = 0 corresponds to zero volume and is therefore rejected. So the maximum occurs at x = 3 2
Which implies that ϕ = 2 π 3 2 = 2 9 3 . 9 4 ∘