Building it up.
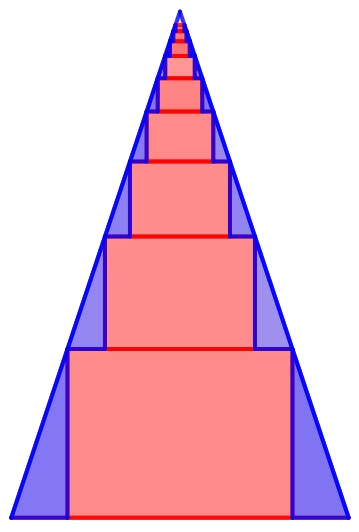
Let R 0 and H 0 be the radius and height of the initial right circular cone C 1 . Find the volume V 1 of the largest right circular cylinder with radius r 1 and height h 1 that can be inscribed in the initial cone C 1 .
Now, let r 1 and H 1 = H 0 − h 1 be the radius and height of the remaining right circular cone C 2 . Find the volume V 2 of the largest right circular cylinder with radius r 2 and height h 2 that can be inscribed in the remaining cone C 2 .
In general for n ≥ 2 : Let r n − 1 and H n − 1 = H n − 2 − h n − 1 be the radius and height of the remaining right circular cone C n . Find the volume V n of the largest right circular cylinder with radius r n and height h n that can be inscribed in the remaining cone C n .
Find V = n = 1 ∑ ∞ V n and let V ∗ be the total volume of the blue regions. If V cone is the volume of the initial right circular cone and V cone V ∗ = β α , where α and β are coprime positive integers, find α + β .
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the volume of the cone V c o n e = 3 1 π R 0 2 H 0 and the volume of the cylinder V 1 = π r 1 2 h 1 .
From the geometry of the problem we have two similar triangles whose proportion is: R 0 − r − 1 R 0 = h 1 H 0 ⟹
h 1 = R 0 H 0 ( R 0 − r 1 ) ⟹ V 1 = R 0 H 0 π ∗ ( R 0 r 1 2 − r 1 3 ) ⟹
d r 1 d V 1 = R 0 H 0 π ∗ r 1 ∗ ( 2 R 0 − 3 r 1 ) = 0 , r 1 = 0 ⟹ r 1 = 3 2 R 0 .
d r 1 2 d 2 V 1 = R 0 H 0 π ∗ ( 2 R 0 − 6 r 1 ) and d r 1 2 d 2 V 1 ∣ r 1 = 3 2 R 0 = R 0 − 2 H 0 π < 0 ⟹ we have a maximum at r 0 = 3 2 R 0
and r 1 = 3 2 R 0 ⟹ h 1 = 3 H 0
⟹
r 2 = 3 2 r 1 = ( 3 2 ) 2 R 0 , H 1 = H 0 − h 1 = 3 2 H 0 ⟹ h 2 = r 1 H 1 ( r 1 − r 2 ) = 3 2 2 H 0
⟹ r 3 = 3 2 r 2 = ( 3 2 ) 3 R 0 , H 2 = H 1 − h 2 = ( 3 2 ) 2 H 0 ⟹ h 3 = r 2 H 2 ( r 2 − r 3 ) = 3 2 2 2 H 0
For n ≥ 1 r n = ( 3 2 ) n R 0 , H n − 1 = ( 3 2 ) n − 1 H 0 and h n = 3 1 ( 3 2 ) n − 1 H 0 and
∑ n = 1 ∞ h n = 3 H 0 ∑ n = 1 ∞ ( 3 2 ) n − 1 = H 0
⟹ V n = ( 2 3 ) ( 2 7 8 ) n V c o n e ⟹ V = ∑ n = 1 ∞ V n = 2 3 V 0 ∑ n = 1 ∞ ( 2 7 8 ) n = 1 9 1 2 V c o n e
and,
V ∗ = V c o n e − V = V c o n e ( 1 − 1 9 1 2 ) = 1 9 7 V c o n e ⟹ V c o n e V ∗ = 1 9 7 = β α ⟹ α + β = 2 6 .
improve more
Since the answer we need is a ratio, for the ease of calculation, we can take H 0 = 1 and R 0 = 1 , therefore V cone = 2 1 π H 0 R 0 2 = 3 π .
Considering r 1 and h 1 , due to similar triangles R 0 − r 1 h 1 = R 0 H 0 ⟹ 1 − r 1 h 1 = 1 1 ⟹ h 1 = 1 − r 1 . Then the V 1 is given by:
V 1 d r 1 d V 1 d r 1 2 d 2 V 1 = π r 1 2 h 1 = π r 1 2 ( 1 − r 1 ) = π ( r 1 2 − r 1 3 ) = π ( 2 r 1 − 3 r 1 2 ) = π ( 2 − 6 r 1 ) Differentiate both sides w.r.t. r 1 and
⟹ d r 1 d V 1 = 0 , when r 1 = 0 or r 1 = 3 2 . This means that V 1 is maximum when r 1 = 3 2 , since d r 1 2 d 2 V 1 ∣ ∣ ∣ ∣ r 1 = 3 2 < 0 .
Similarly, we have r 2 = 3 2 r 1 = ( 3 2 ) 2 r 0 , where r 0 = R 0 = 1 , r 3 = ( 3 2 ) n r 0 , ⟹ r n = ( 3 2 ) n r 0 . Similarly, h n = r n − 1 − r n . And V n = π r n 2 h n = π r n 2 ( r n − 1 − r n ) . Therefore,
V = n = 1 ∑ ∞ V n = n = 1 ∑ ∞ π r n 2 ( r n − 1 − r n ) = π n = 1 ∑ ∞ ( 3 2 ) 2 n ( ( 3 2 ) n − 1 − ( 3 2 ) n ) = π n = 1 ∑ ∞ ( 3 2 ) 3 n − 1 ( 1 − 3 2 ) = 2 π n = 1 ∑ ∞ ( 2 7 8 ) n = 2 π ⋅ 2 7 8 ( 1 − 2 7 8 1 ) = 1 9 4 π Since r n = ( 3 2 ) n
Therefore, V cone V ∗ = V cone V cone − V = 1 − V cone V = 1 − 3 1 1 9 4 = 1 − 1 9 1 2 = 1 9 7 . Hence α + β = 7 + 1 9 = 2 6 .