Buoy Riddle

Solution Using Pythagorean Theorem:

$R^2=24^2+(R-18)^2$

$R^2=576+R^2-36R+324$

$R^2=900+R^2-36R$

$36R=900$

$\large\boxed{R=25}$ $\color{#D61F06}\large \boxed{\text{answer}}$

Relevant wiki: Extended Sine Rule

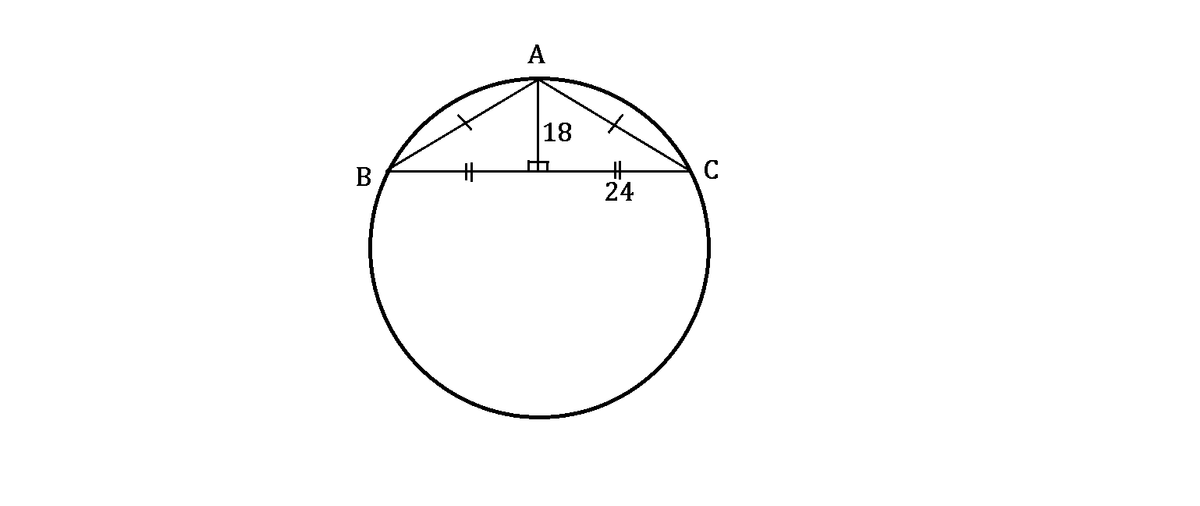
By constructing a 2-D inscribed triangle $ABC$ in the spherical section, as shown above, we can calculate $AC = \sqrt{18^2 + 24^2} = 30$ .

Then $\sin \angle C = \dfrac{18}{30}$

Thus, by Sine Rule , $\dfrac{30}{\sin \angle C} = \dfrac{30^2}{18} = 2R$ , where $R$ is the radius of the circumcircle and, in this case, the sphere.

Hence, $R = \dfrac{30^2}{6^2} = \boxed{25}$ .

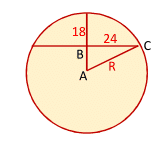In triangle $ABC$

$R^2=(R-18)^2+24^2$

Solution is $R=25$ .

Relevant wiki: Pythagorean Theorem

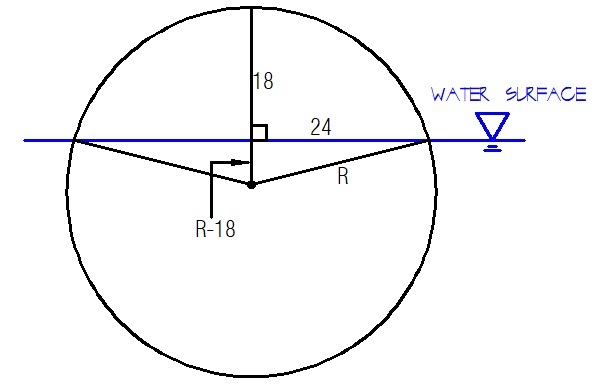By pythagorean theorem, we have

$R^2=(R-18)^2+24^2$

$R^2=R^2-36R+324+576$

$36R=900$

$\boxed{R=25}$

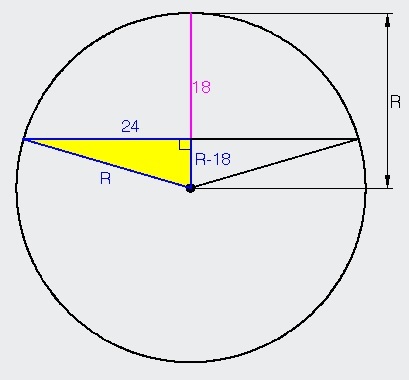Applying pythagorean theorem on the yellow right triangle, we have

$R^2=(R-18)^2+24^2$

$R^2=R^2-36R+324R+576$

$36R=900$

$\color{#D61F06}\large \boxed{R=25}$

If we drop a line from the top of the ball T to the bottom B and call the point where the radius meets the sphere A and the point where the radius meets the diameter we've drawn C then the angle TAB = 90 degrees. tan of angle TAC = 18 / 24 = .75 so angle TAC = 36.8699 degrees. angle CAB = 90 - TAC = 53.1301 degrees and 24 times tan (53.1301) = 32 for line CB so diameter TB = TC + CB = 18 + 32 and radius = 25