Buoyancy + Force +Pressure!
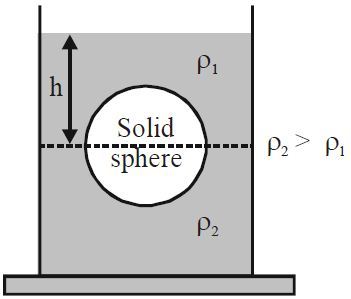 A solid sphere of radius
r
is floating at the interface of two immiscible liquids of densities
ρ
1
and
ρ
2
where
ρ
2
>
ρ
1
, half of its volume lying in each zone. The height of the upper liquid column from the interface of the two liquids is
h
.
A solid sphere of radius
r
is floating at the interface of two immiscible liquids of densities
ρ
1
and
ρ
2
where
ρ
2
>
ρ
1
, half of its volume lying in each zone. The height of the upper liquid column from the interface of the two liquids is
h
.
Find the force exerted on the sphere by contact with the upper liquid layer.
Details
- atmospheric pressure = p 0
- acceleration due to gravity is g
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Ahhhhh of course... I did it the hard way:
F = 2 π h − r ∫ h ( P o + ρ 1 g x ) ( h − x ) d x
Shoot, this one got me; the second fluid threw me off. But at least I know now.